题目内容
7．已知函数f（x）=xlnx-ax2在（0，+∞）上单调递减，则实数a的取值范围是[$\frac{1}{2}$，+∞）．分析 求出函数的导数，问题转化为即a≥$\frac{lnx+1}{2x}$在（0，+∞）恒成立，令g（x）=$\frac{lnx+1}{2x}$，x∈（0，+∞），根据函数的单调性求出a的范围即可．
解答 解：f′（x）=lnx-2ax+1，
若f（x）在（0，+∞）递减，
则lnx-2ax+1≤0在（0，+∞）恒成立，
即a≥$\frac{lnx+1}{2x}$在（0，+∞）恒成立，
令g（x）=$\frac{lnx+1}{2x}$，x∈（0，+∞），
g′（x）=-$\frac{lnx}{{2x}^{2}}$，
令g′（x）＞0，解得：0＜x＜1，
令g′（x）＜0，解得：x＞1，
故g（x）在（0，1）递增，在（1，+∞）递减，
故g（x）max=g（1）=$\frac{1}{2}$，
故a≥$\frac{1}{2}$，
故答案为：[$\frac{1}{2}$，+∞）．
点评 本题考查了函数的单调性、最值问题，考查导数的应用以及函数恒成立问题，是一道中档题．
练习册系列答案
相关题目
2．若双曲线$\frac{x^2}{3-m}+\frac{y^2}{m-1}=1$的渐近线方程为$y=±\frac{1}{2}x$，则m的值为（ ）
| A． | -1 | B． | $\frac{1}{3}$ | C． | $\frac{11}{3}$ | D． | -1或$\frac{1}{3}$ |
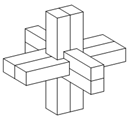如图为中国传统智力玩具鲁班锁，起源于古代汉族建筑中首创的榫卯结构，这种三维的拼插器具内部的凹凸部分（即榫卯结构）啮合，外观看是严丝合缝的十字立方体，其上下、左右、前后完全对称，六根完全相同的正四棱柱分成三组，经90°榫卯起来．现有一鲁班锁的正四棱柱的底面正方形边长为1，欲将其放入球形容器内（容器壁的厚度忽略不计），若球形容器表面积的最小值为30π，则正四棱柱体的高为（ ）