题目内容

16．求椭圆$\frac{{x}^{2}}{64}$+$\frac{{y}^{2}}{36}$=1的长轴长、短轴长、顶点坐标、离心率．

分析 利用椭圆$\frac{{x}^{2}}{64}$+$\frac{{y}^{2}}{36}$=1，可得a2=64，b2=36，即可得到a，b，c，进而得到长轴长、短轴长、顶点坐标、离心率．

解答 解：∵椭圆$\frac{{x}^{2}}{64}$+$\frac{{y}^{2}}{36}$=1，∴a2=64，b2=36．
∴a=8，b=6，c=2$\sqrt{7}$．
∴椭圆的长轴和短轴的长分别为2a=16，2b=12．
顶点（±8，0），（0，±6）．
离心率e=$\frac{c}{a}$=$\frac{\sqrt{7}}{4}$．

点评 熟练掌握椭圆的标准方程及其性质是解题的关键．

练习册系列答案
相关题目
9．给出下列结论：
①函数y=2x2-1在x=3处的导数为11；
②若物体的运动规律是s=f（t），则物体在时刻t0的瞬时速度v等于f′（t0）；
③物体做直线运动时，它的运动规律可以用函数v=v（t）描述，其中v表示瞬时速度，t表示时间，那么该物体运动的加速度为a=$\underset{lim}{△t→0}$$\frac{v（t+△t）-v（t）}{△t}$；
④若f（x）=$\sqrt{x}$，则f′（0）=0．
其中正确的结论序号为②③．
7．已知偶函数y=f（x）的定义域为R，且对任意实数x，恒有f（$\frac{1}{2}$+x）=f（$\frac{1}{2}$-x），当x∈[0，$\frac{1}{2}$]，f（x）=（x-$\frac{1}{2}$）2．
（1）求证：f（x）为周期函数；
（2）当x∈R时，求f（x）的解析式；
（3）解不等式f（sinx）＜f（cosx）．
4．下列结论正确的是（　　）
A．（5x）'=5xB．（5x）'=5xln5C．$（{log_a}x）'=\frac{lna}{x}$D．．$（{log_a}x）'=\frac{a}{x}$
11．下列四个命题：
（1）命题“若a=0，则ab=0”的否命题是“若a=0，则ab≠0”；
（2）若命题p：?x∈R，x2+x+1＜0，则?p：?x∈R，x2+x+1≥0；
（3）若命题“?p”与命题“p或q”都是真命题，则命题q一定是真命题；
（4）命题“若0＜a＜1，则“loga（a+1）＜loga（1+$\frac{1}{a}$）”是真命题．
（5）“φ=$\frac{π}{2}$”是“y=sin（2x+φ）为偶函数”的充要条件
其中真命题的有几个（　　）
A．0B．1C．2D．3
1．已知f（cosx）=cos5x，则f（sin30°）=$\frac{1}{2}$．
8．袋子中装有大小相同的5个小球，分别有2个红球3个白球，现从中随机抽取2个小球，则这2个球中既有红球也有白球的概率为（　　）
A．$\frac{3}{4}$B．$\frac{7}{10}$C．$\frac{4}{5}$D．$\frac{3}{5}$
5．函数f（x）=|x+2|的单调递增区间是[-2，+∞）．
6．执行如图所示的程序框图，其中m=1007${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$cosxdx，则输出a的结果为（　　）
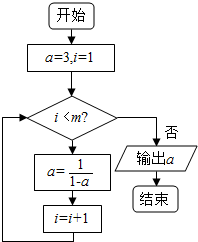
A．3B．-$\frac{1}{2}$C．$\frac{2}{3}$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网