��Ŀ����
11�������ĸ����⣺��1�����⡰��a=0����ab=0���ķ������ǡ���a=0����ab��0����
��2��������p��?x��R��x2+x+1��0����?p��?x��R��x2+x+1��0��
��3�������⡰?p�������⡰p��q�����������⣬������qһ���������⣻
��4�����⡰��0��a��1����loga��a+1����loga��1+$\frac{1}{a}$�����������⣮
��5������=$\frac{��}{2}$���ǡ�y=sin��2x+�գ�Ϊż�������ij�Ҫ����
����������������������
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� ��1�����÷�����Ķ��弴���жϳ�����
��2������?p�Ķ��弴���жϳ���
��3�������⡰?p�������⡰p��q�����������⣬�ɵ�����p�Ǽ����⣬qһ���������⣬�����жϳ�����
��4����0��a��1����a+1��1+$\frac{1}{a}$������y=logax�ĵ����Լ����жϳ�����
��5������=k��+$\frac{��}{2}$����k��Z�����ǡ�y=sin��2x+�գ�Ϊż�������ij�Ҫ�����������жϳ�����
��� �⣺��1�����⡰��a=0����ab=0���ķ������ǡ���a��0����ab��0������˲���ȷ��
��2��������p��?x��R��x2+x+1��0����?p��?x��R��x2+x+1��0����ȷ��
��3�������⡰?p�������⡰p��q�����������⣬������p�Ǽ����⣬qһ���������⣬��ȷ��
��4����0��a��1����a+1��1+$\frac{1}{a}$����loga��a+1����loga��1+$\frac{1}{a}$�����Ǽ����⣬����ȷ��
��5������=k��+$\frac{��}{2}$����k��Z�����ǡ�y=sin��2x+�գ�Ϊż�������ij�Ҫ��������˲���ȷ��
�������������2����
��ѡ��C��
���� ���⿼���˼��������ж������������ĵ����ԣ�������������������������������е��⣮

 ��У����ϵ�д�
��У����ϵ�д�| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{5}$ | D�� | $\frac{1}{6}$ |
| A�� | ���⡰��P�������⡰��q������ٲ�ͬ | B�� | ����P�����⡰��q���������ͬ | ||
| C�� | ����q�����⡰��P���������ͬ | D�� | ���⡰��P�ҷ�q���������ͬ |
| A�� | $\frac{1}{2}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{3}{4}$ | D�� | 1 |
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
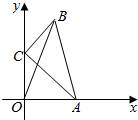 ��ƽ��ֱ������ϵ�У���ABC���㣺��C=90�㣬AC=2��BC=1����A��C�ֱ���x�ᡢy���ϣ�����A��ԭ�㿪ʼ��x������������˶�ʱ����C������y�����˶���
��ƽ��ֱ������ϵ�У���ABC���㣺��C=90�㣬AC=2��BC=1����A��C�ֱ���x�ᡢy���ϣ�����A��ԭ�㿪ʼ��x������������˶�ʱ����C������y�����˶���