题目内容
13.圆C的极坐标方程为ρ=4$\sqrt{2}$sin(θ+$\frac{π}{4}$)的直角坐标方程为x2+y2-4x-4y=0分析 先将原极坐标方程中的三角函数式利用三角函数的和角公式化开后再化成直角坐标方程即可.
解答 解:将原极坐标方程为ρ=4$\sqrt{2}$sin(θ+$\frac{π}{4}$),
化成:ρ=4sinθ+4cosθ,其直角坐标方程为:
∴x2+y2-4x-4y=0.
故答案为x2+y2-4x-4y=0.
点评 本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
相关题目
3.已知复数$z=\frac{5}{2-i}$(i是复数单位),则复数z为( )
| A. | 2+i | B. | -2+i | C. | -2-i | D. | 2-i |
4.有一段“三段论”,其推理是这样的:
对于可导函数f(x),若f′(x0)=0,则x=x0是函数f(x)的极值点…大前提因为函数f(x)=x3满足f′(0)=0,…小前提所以x=0是函数f(x)=x3的极值点”,结论以上推理( )
对于可导函数f(x),若f′(x0)=0,则x=x0是函数f(x)的极值点…大前提因为函数f(x)=x3满足f′(0)=0,…小前提所以x=0是函数f(x)=x3的极值点”,结论以上推理( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 没有错误 |
8.如果a<b<0,那么下列不等式成立的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | a+c<b+c | C. | a-c>b-c | D. | a•c<b•c |
18.等差数列{an}的前n项和Sn,若a1=2,S5=15,则a19=( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
5.用数学归纳法证明“1+2+22+…+2n+2=2n+3-1”,验证n=1时,左边计算所得的式子为( )
| A. | 1 | B. | 1+2 | C. | 1+2+22 | D. | 1+2+22+23 |
2.方程$|sin\frac{π}{2}x|=lg|x|$有多少个根?( )
| A. | 9 | B. | 10 | C. | 18 | D. | 20 |
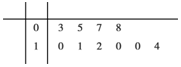 学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下:
学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下: