题目内容
19.已知f(x)=asin2x-$\frac{1}{3}$sin3x(a为常数),在x=$\frac{π}{3}$处取得极值,则a=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $-\frac{1}{2}$ |
分析 先对函数进行求导,根据函数f(x)在x=$\frac{π}{3}$处有极值应有f′($\frac{π}{3}$)=0,进而可解出a的值.
解答 解:f′(x)=2acos2x-cos3x,
根据函数f(x)在x=$\frac{π}{3}$处有极值,故应有f′($\frac{π}{3}$)=0,
即2acos$\frac{2π}{3}$-cos(3×$\frac{π}{3}$)=-2×$\frac{1}{2}$a+1=-a+1=0
解得a=1,
故选:B.
点评 本题主要考查函数在某点取得极值的条件,属基础题.

练习册系列答案
相关题目
8.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,6秒旋转一周.已知时间t=0时,点A的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),则当0≤t≤6时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
| A. | [0,1] | B. | [4,6] | C. | [1,3] | D. | [0,1]和[4,6] |
9.甲乙两位同学同住一小区,甲乙俩同学都在7:00~7:20经过小区门口.由于天气下雨,他们希望在小区门口碰面结伴去学校,并且前一天约定先到者必须等候另一人5分钟,过时即可离开.则他俩在小区门口碰面结伴去学校的概率是( )
| A. | $\frac{5}{9}$ | B. | $\frac{6}{11}$ | C. | $\frac{8}{15}$ | D. | $\frac{7}{16}$ |
 已知抛物线x2=4y,圆C:x2+(y-2)2=4,点M(x0,y0),(x0>0,y0>4)为抛物线上的动点,过点M的圆C的两切线,设其斜率分别为k1,k2
已知抛物线x2=4y,圆C:x2+(y-2)2=4,点M(x0,y0),(x0>0,y0>4)为抛物线上的动点,过点M的圆C的两切线,设其斜率分别为k1,k2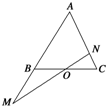 如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$ (m,n>0),则m2+n的范围为[$\frac{7}{4}$,4).
如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$ (m,n>0),则m2+n的范围为[$\frac{7}{4}$,4).