题目内容
函数y=ax-1+1 （a＞0且a≠1）的图象恒过定点P，则P点的坐标是 ．
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：解析式中的指数x-1=0求出x的值，再代入解析式求出y的值，即得到定点的坐标．
解答：
解：由于函数y=ax经过定点（0，1），令x-1=0，可得x=1，求得f（1）=2，
故函数f（x）=ax-1+1（a＞0，a≠1），则它的图象恒过定点的坐标为（1，2），
故答案为 （1，2）．
故函数f（x）=ax-1+1（a＞0，a≠1），则它的图象恒过定点的坐标为（1，2），
故答案为 （1，2）．
点评：本题主要考查指数函数的图象过定点（0，1）的应用，即令解析式中的指数为0，求出对应的x和y的值，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
，则f（2-log
3）=（ ）
|
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合M{x|x2-x＞0}，N={0，1，2，3}，则（∁UM）∩N=（ ）
| A、{x|0≤x≤1} |
| B、{0，1} |
| C、{2，3} |
| D、{1，2，3} |
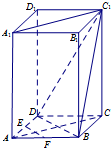在长方体ABCD-A1B1C1D1中，底面ABCD为正方形，E，F分别为棱AD、，AB的中点．