题目内容
9.已知函数f(x)=$\left\{\begin{array}{l}{|x-1|-2}&{|x|≤1}\\{\frac{1}{1+{x}^{2}}}&{|x|>1}\end{array}\right.$,若f(a)=$\frac{1}{5}$,求a的值.分析 直接利用分段函数以及方程求解即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{|x-1|-2}&{|x|≤1}\\{\frac{1}{1+{x}^{2}}}&{|x|>1}\end{array}\right.$,若f(a)=$\frac{1}{5}$,
当|a|≤1,即-1≤a≤1时,|a-1|-2=$\frac{1}{5}$,解得a=$-\frac{6}{5}$或$\frac{16}{5}$,不满足题意.
当|a|>1,即-1>a,或a>1时,$\frac{1}{1+{a}^{2}}=\frac{1}{5}$,解得a=-2或2,满足题意.
综上,a的值为:±2.
点评 本题考查分段函数的应用,方程的解与根的关系,考查计算能力.

练习册系列答案
相关题目
20.已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<0)的图象的相邻两个对称中心的坐标分别为($\frac{π}{9}$,0),($\frac{4π}{9}$,0),为了得到f(x)的图象,只需将g(x)=2sinωx的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{9}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{9}$个单位 |
14.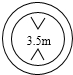 图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )
图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )
 图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )
图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )| A. | h≤3.5 | B. | h≥3.5 | C. | h<3.5 | D. | h>3.5 |
18.小明身高比小强高,小强身高比小丽高,那么小明身高比小丽高,上述描述符号不等式的哪个性质( )
| A. | 如果a>b,那么b<a;如果b<a,那么a>b | |
| B. | 如果a>b,b>c,那么a>c | |
| C. | 如果a>b,那么a+c>b+c | |
| D. | 如果a>b,c>0,那么ac>bc |