题目内容

设（5x-
1
x
）4的展开式的各项系数之和为M，二项式系数之和为N，则M-N=（　　）
A、-240B、150
C、0D、240
考点：二项式系数的性质
专题：计算题,二项式定理
分析：由二项展开式的性质可得M=44，N=24，即可得出结论．
解答： 解：由二项展开式的性质可得M=44，N=24
∴M-N=240．
故选：D．
点评：解题的关键是利用二项式的性质得出M，N的值．
练习册系列答案
相关题目
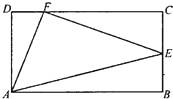如图所示，有一个长AB=4，宽BC=2的矩形木料ABCD，E为BC的中点，点F在边CD上．一木工师傅想在该木料上取满足∠EAF=
π
3
的一个△AEF，设F与D的距离为x，则满足条件的x所在的范围是（　　）
A、（
3
4
，1）
B、（
1
2
，
3
4
）
C、（
1
4
，
1
2
）
D、（0，
1
4
）
已知条件p：|x-1|＜2，条件q：x2-3x-4＜0，则条件p成立是条件q成立的（　　）
A、充分不必要
B、必要不充分
C、充要
D、既不充分也不必要
已知命题p：?x∈（1，+∞），函数f（x）=log2（x+1）-1有零点；命题q：若a=（1，2），b=（-2，-4），则a∥b，下列命题为真命题的是（　　）
A、p∧q
B、p∨（￢q）
C、（￢p）∧q
D、p∧（￢q）
已知|
a
|=
3
，|
b
|=1，
a
与
b
的夹角为30°，则|
a
-2
b
|=（　　）
A、1
B、
2
C、
3
D、2
某校共有400名学生参加了一次数学竞赛，竞赛成绩的频率分布直方图如图所示，则在本次竞赛中，得分不低于80分的人数为（　　）
A、240B、160
C、120D、100
（文科）设集合A={（x，y）|x-y=0}，B={（x，y）|2x-3y+4=0}，则A∩B=（　　）
A、{（4，4）}
B、{4，4}
C、（4，4）
D、{（4）}
某大学数学系共有本科生1000人，其中一、二、三、四年级的人数比为4：3：2：1，要用分层抽样的方法从所有本科生中抽取一个容量为200的样本，则应抽取三年级的学生人数为（　　）
A、80B、40C、60D、20
设{an}为等差数列，且a3+a9=12，则S11=（　　）
A、55B、66C、77D、88

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网