题目内容
5.如果实数x,y满足$\left\{\begin{array}{l}{2x-y-6≤0}\\{x+y-3≥0}\\{y≤3}\end{array}\right.$,则z=x+2y的最大值为( )| A. | -6 | B. | 3 | C. | 6 | D. | $\frac{21}{2}$ |
分析 先根据约束条件画出可行域,设z=x+2y,再利用z的几何意义求最值,只需求出直线z=x+2y过可行域内的点B时,从而得到z值即可.
解答 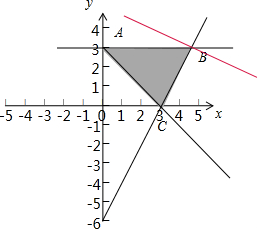 解:先根据约束条件实数x,y满足$\left\{\begin{array}{l}{2x-y-6≤0}\\{x+y-3≥0}\\{y≤3}\end{array}\right.$,画出可行域,设z=x+2y,
解:先根据约束条件实数x,y满足$\left\{\begin{array}{l}{2x-y-6≤0}\\{x+y-3≥0}\\{y≤3}\end{array}\right.$,画出可行域,设z=x+2y,
将最大值转化为y轴上的截距,
由$\left\{\begin{array}{l}{y=3}\\{2x-y-6=0}\end{array}\right.$得B($\frac{9}{2}$,3).
当直线z=x+2y经过点B($\frac{9}{2}$,3)时,z最大,
数形结合,将点B的坐标代入z=$\frac{9}{2}$+2×3=$\frac{21}{2}$得
z最大值为:$\frac{21}{2}$,
故选:D.
点评 本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.

练习册系列答案
相关题目
20.要得到y=$\sqrt{3}$cos2x+sinxcosx的图象,只需把y=sin2x的图象上所有点( )
| A. | 向左平移$\frac{π}{6}$个单位,再向上移动$\frac{\sqrt{3}}{2}$个单位 | |
| B. | 向左平移$\frac{π}{3}$个单位,再向上移动$\frac{\sqrt{3}}{2}$个单位 | |
| C. | 向右平移$\frac{π}{6}$个单位,再向下移动$\frac{\sqrt{3}}{2}$个单位 | |
| D. | 向右平移$\frac{π}{3}$个单位,再向下移动$\frac{\sqrt{3}}{2}$个单位 |
10.已知某一离散型随机变量X的分布如表所示:
则E(X)=2.45.
| X | 1 | 2 | 3 | 4 |
| P | a | a+0.03 | a-0.01 | a-0.02 |
17.函数f(x)=-$\frac{1}{3}$x3+4x-4在[0,3]上的最大值为( )
| A. | -4 | B. | -1 | C. | $\frac{4}{3}$ | D. | 2 |
15.用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短,最短的篱笆是( )?
| A. | 30 | B. | 36 | C. | 40 | D. | 50 |