题目内容
6．点M为棱长是$2\sqrt{2}$的正方体ABCD-A1B1C1D1的内切球O球面上的动点，点N为B1C1的中点，若满足DM⊥BN，则动点M的轨迹的长度为$\frac{{4\sqrt{10}π}}{5}$．分析 直线DM在过点D且与BN垂直的平面内．又点M在内接球的球面上，故点M的轨迹是正方体的内切球与过D且与BN垂直的平面相交得到的小圆，即可得出结论．
解答 解：设BB1的中点E，CE为DM在平面B1C1CB中的射影，直线DM在过点D且与BN垂直的平面内．
又点M在内接球的球面上，
故点M的轨迹是正方体的内切球与过D且与BN垂直的平面相交得到的小圆，
即点M的轨迹为过D，C，E的平面与内切球的交线．
由等面积$\frac{1}{2}×\sqrt{10}×h=\frac{1}{2}×\sqrt{2}×\sqrt{2}$，
求得点O到此平面的距离为$\frac{\sqrt{10}}{5}$，截得小圆的半径为$\frac{2\sqrt{10}}{5}$，
所以以点P的轨迹的长度为$\frac{{4\sqrt{10}π}}{5}$，
故答案为$\frac{{4\sqrt{10}π}}{5}$．
点评 本题考查了学生的空间想象力，求出点M的轨迹是关键，属于中档题．
练习册系列答案
相关题目
15．已知函数f（x）=$\left\{\begin{array}{l}{|lo{g}_{2}x|，0＜x＜2}\\{sin（\frac{π}{4}x），2≤x≤10}\end{array}\right.$，若存在实数x1，x2，x3，x4满足f（x1）=f（x2）=f（x3）=f（x4），且x1＜x2＜x3＜x4，则$\frac{（{x}_{3}-1）•（{x}_{4}-1）}{{x}_{1}•{x}_{2}}$的取值范围是（ ）
| A． | （9，21） | B． | （20，32） | C． | （8，24） | D． | （15，25） |
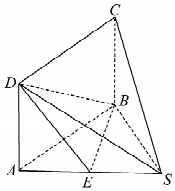如图，在四棱锥S-ABCD中，四边形ABCD为矩形，E为SA的中点，SB=2，BC=3，$SC=\sqrt{13}$．
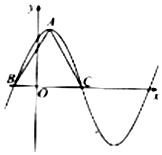函数f（x）=6cos2$\frac{ωx}{2}$+$\sqrt{3}$sinωx-3（ω＞0）在一个周期内的图象如图所示，A为图象的最高点，B，C为图象与x轴的交点，且△ABC为正三角形．
16．已知函数f（x）=（2-x）ex-ax-a，若不等式f（x）＞0恰有两个正整数解，则a的取值范围是（ ）
| A． | [-$\frac{1}{4}$e3，0） | B． | [-$\frac{1}{2}$e，0） | C． | [-$\frac{1}{4}$e3，$\frac{e}{2}$） | D． | [-$\frac{1}{4}$e3，2） |