题目内容
16.已知函数f(x)=(2-x)ex-ax-a,若不等式f(x)>0恰有两个正整数解,则a的取值范围是( )| A. | [-$\frac{1}{4}$e3,0) | B. | [-$\frac{1}{2}$e,0) | C. | [-$\frac{1}{4}$e3,$\frac{e}{2}$) | D. | [-$\frac{1}{4}$e3,2) |
分析 利用构造的新函数g(x)和h(x),求导数g′(x),从而可得a的范围.
解答 解:令g(x)=(2-x)ex,h(x)=ax+a,
由题意知,存在2个正整数,使g(x)在直线h(x)的上方,
∵g′(x)=(1-x)ex,
∴当x>1时,g′(x)<0,当x<1时,g′(x)>0,
∴g(x)max=g(1)=e,
且g(0)=2,g(2)=0,g(3)=-e3,
直线h(x)恒过点(-1,0),且斜率为a,
由题意可知,$\left\{\begin{array}{l}{h(1)<e}\\{h(2)<0}\\{h(3)≥-{e}^{3}}\end{array}\right.$,
故实数a的取值范围是[-$\frac{1}{4}$e3,0),
故选A.
点评 本题考查导数的综合应用,及数形结合思想的应用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
4.有一段“三段论”,其推理是这样的:
对于可导函数f(x),若f′(x0)=0,则x=x0是函数f(x)的极值点…大前提因为函数f(x)=x3满足f′(0)=0,…小前提所以x=0是函数f(x)=x3的极值点”,结论以上推理( )
对于可导函数f(x),若f′(x0)=0,则x=x0是函数f(x)的极值点…大前提因为函数f(x)=x3满足f′(0)=0,…小前提所以x=0是函数f(x)=x3的极值点”,结论以上推理( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 没有错误 |
11.已知$\overrightarrow a$,$\overrightarrow b$满足:$|\overrightarrow a|=3$,$|\overrightarrow b|=2$,$\overrightarrow a•\overrightarrow b=\frac{3}{2}$,则$|\overrightarrow a-\overrightarrow b|$=( )
| A. | $\sqrt{10}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 10 |
8.如果a<b<0,那么下列不等式成立的是( )
| A. | $\frac{1}{a}<\frac{1}{b}$ | B. | a+c<b+c | C. | a-c>b-c | D. | a•c<b•c |
5.用数学归纳法证明“1+2+22+…+2n+2=2n+3-1”,验证n=1时,左边计算所得的式子为( )
| A. | 1 | B. | 1+2 | C. | 1+2+22 | D. | 1+2+22+23 |
6.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有3f(x)+xf′(x)>0,则不等式(x+2017)3f(x+2017)+27f(-3)>0的解集是( )
| A. | (-2020,-2017) | B. | (-∞,-2017) | C. | (-2018,-2017) | D. | (-∞,-2020) |
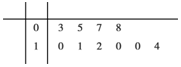 学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下:
学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下: