题目内容
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2+x+1，求f（x）的解析式．
考点：函数奇偶性的性质
专题：常规题型,函数的性质及应用
分析：要求f（x）的解析式，只要求出x＜0的解析式即可，设x＜0，则-x＞0，代入x＞0的解析式，然后利用函数f（x）是奇函数得到f（-x）=-f（x），即可求出f（x）在x＜0时的解析式．
解答：
解：设x＜0，则-x＞0
∴f（-x）=（-x）2+（-x）+1=x2-x+1
又∵f（x）是定义在R上的奇函数，
∴f（-x）=-f（x）
∴-f（x）=x2-x+1
即f（x）=-x2+x-1
∴f（x）=
．
∴f（-x）=（-x）2+（-x）+1=x2-x+1
又∵f（x）是定义在R上的奇函数，
∴f（-x）=-f（x）
∴-f（x）=x2-x+1
即f（x）=-x2+x-1
∴f（x）=
|
点评：本题是知道函数一个区间上的解析式，求另外区间上的解析式，关键是利用函数的奇偶性进行转化．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
已知函数f（x）=aln（x+1）-x2，在区间（-1，0）内任取两个实数p，q，且p≠q，若不等式
＞1恒成立，则实数a的取值范围为（ ）
| f(p+1)-f(q+1) |
| p-q |
| A、[6，+∞） | ||
| B、[4，+∞） | ||
C、[-
| ||
| D、[1，+∞） |
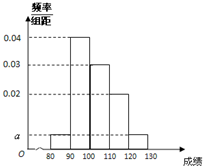为了分析我校市二模文科数学的成绩，现抽样统计了20位同学的数学成绩，形成了如图所示的频率分布直方图，其中成绩的分组区间是：[80，90），[90，100），[100，110），[110，120），[120，130]