题目内容
设定义在R上的函数f(x)=
,若关于x的方程f2(x)+bf(x)+c=0有3个不同的实数解x1,x2,x3,则x1+x2+x3等于( )
|
| A、3 | B、6 | C、-b-1 | D、c |
考点:分段函数的应用
专题:函数的性质及应用
分析:先画出f(x)的图象,观察图形可知若关于x的方程f2(x)+af(x)+b=3有三个不同实数解满足的条件,然后图象对称性求出三个根即可.
解答:
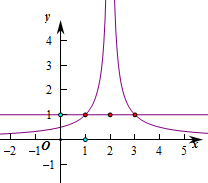 解:分段函数的图象如图所示:
解:分段函数的图象如图所示:
由图可知,只有当f(x)=1时,它有三个根.
由
=1,即|x-2|=1,
解得x=1,x=2或x=3.
∴关于x的方程f2(x)+af(x)+b=0有且只有3个不同实数解,不妨设x1<x2<x3,
解分别是1,2,3,即x1=1,x2=2,x3=3,
∴x1+x2+x3=1+2+3=6,
故选:B
 解:分段函数的图象如图所示:
解:分段函数的图象如图所示:由图可知,只有当f(x)=1时,它有三个根.
由
| 1 |
| |x-2| |
解得x=1,x=2或x=3.
∴关于x的方程f2(x)+af(x)+b=0有且只有3个不同实数解,不妨设x1<x2<x3,
解分别是1,2,3,即x1=1,x2=2,x3=3,
∴x1+x2+x3=1+2+3=6,
故选:B
点评:本题主要考查了函数与方程的综合运用,以及函数的图象与方程之间的关系,利用数形结合是解决本题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
若
(2x-3x2)dx=0,则k=( )
| ∫ | k 0 |
| A、1 | B、0 |
| C、0或1 | D、以上都不对 |
若复数m2-2m-3+(m2-3m-4)i为纯虚数(i为虚数单位),则实数m=( )
| A、m=-1 |
| B、m=3 |
| C、m=-1或 m=3 |
| D、m=0 |
判定下列命题
①第一象限的角为锐角
②f(x)=xcosx为奇函数
③
-
=
④(
•
)•
=
•(
•
)
正确的为( )
①第一象限的角为锐角
②f(x)=xcosx为奇函数
③
| AB |
| AC |
| CB |
④(
| a |
| b |
| c |
| a |
| b |
| c |
正确的为( )
| A、①② | B、①③ | C、②③ | D、①④ |
已知集合A={x∈R|0<x<1},B={x∈R|(2x-1)(x+1)≤0},则(∁RA)∩B( )
A、[0,
| ||
| B、[-1,0] | ||
C、[
| ||
| D、(-∞,-1]∪[0,+∞) |
设f(x)=
x3+ax2+5x+6在区间[1,3]上单调函数,则实数a的取值范围为( )
| 1 |
| 3 |
A、[-
| ||
| B、(-∞,-3] | ||
C、[-3,
| ||
D、(-∞,-3]∪[-
|
若a=sin2,b=cos2,则a,b的大小为( )
| A、a<b | B、b<a |
| C、a=b | D、不能确定 |
在△ABC中,
=
,
=
,D为BC的中点,则
为( )
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|