题目内容
1.直线x-y-1=0与不等式$\left\{\begin{array}{l}{0≤x≤3}\\{y≥0}\\{x+4y≤16}\end{array}\right.$表示的平面区域的公共整点(横纵坐标均为整数的点)有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 本题考查的知识点是简单线性规划的应用,我们要先画出不等式组表示的平面区域,然后分析平面区域里各个点,进一步求出整点的个数
解答 解:法一,平面区域为梯形OABC(如图所示),
直线x-y-1=0与该区域的公共整点有(1,0),(2,1),(3,2)共三个;
∴选C.
法二,由第一个不等式0≤x≤3得出直线上可能有4个点:(0,-1),(1,0),(2,1),(3,2),
分别带入第二、第三个不等式知(0,-1)点不符合y≥0,排除,只有(1,0),(2,1),(3,2)三个点符合要求,
∴选C.
点评 本题考查了简单线性规划问题的最优解求法;求平面区域的整点个数是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,然后分析平面区域内的点,易求出平面区域内的整点个数

练习册系列答案
相关题目
16.设集合M={1,2},则满足条件M∪N={1,2,6}的集合N的个数是( )
| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
6.设向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,则“$\overrightarrow{a}$•$\overrightarrow{b}$<0”是“θ为钝角”的( )
| A. | 充分不必要条件 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
10.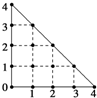 某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)完成下表,并求所种作物的平均年收获量:
(2)在所种年收获量为51或48的作物中随机选取两株求收获量之和,收获量之和为t的概率.
 某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
(1)完成下表,并求所种作物的平均年收获量:
| Y | 51 | 48 | 45 | 42 |
| 频数 |
11.已知函数f(x)=$\frac{1}{2}$x2-2ax+blnx+2a2在x=1处取得极值$\frac{1}{2}$,则a+b=( )
| A. | -1 | B. | 2 | C. | -1或1 | D. | -1或2 |

