题目内容
15．下列说法中正确的有（ ）①幂函数图象均为过点（1，1）；
②幂函数y=x-1在（-∞，0）上单调递减，在（0，+∞）上也单调递减，因此幂函数y=x-1是定义域内的单调函数；
③幂函数的图象均在两个象限内出现；
④幂函数在第四象限内可以有图象；
⑤当a＞0时，幂函数在第一象限内均为增函数；
⑥任意两个幂函数的图象最多有两个交点．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据幂函数的定义和性质分别进行判断即可．
解答 解：①设幂函数为f（x）=xα，则f（1）=1，则幂函数图象均为过点（1，1），故①正确；
②幂函数y=x-1在（-∞，0）上单调递减，在（0，+∞）上也单调递减，因此幂函数y=x-1是定义域内的单调函数，错误，此时函数在定义域（-∞，0）∪（0，+∞）不是单调函数，故②错误；
③当f（x）=${x}^{\frac{1}{2}}$=$\sqrt{x}$时，函数的图象只在第一象限出现，则幂函数的图象均在两个象限内出现错误，故③错误；
④当x＞0时，f（x）=xα＞0，即幂函数不经过第四象限，故④错误；
⑤当a＞0时，幂函数在第一象限内均为增函数，正确；
⑥任意两个幂函数的图象最多有两个交点，错误．
比如f（x）=x2，g（x）=x4，
由x2=x4，得x2（x2-1）=0，得x=0，或x=1或x=-1，即函数有三个交点（0，0），（1，1），（-1，1），故⑥错误，
故正确的是①⑤，共有2个，
故选：B
点评 本题主要考查命题的真假判断，根据幂函数的图象和性质是解决本题的关键．
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
5．某企业生产A、B两种产品，现有资源如下：煤360吨，水300吨，电200千瓦．每生产1吨A产品需消耗煤9吨，水3吨，电4千瓦，利润7万元；每生产1吨B产品需消耗煤4吨，水10吨，电5千瓦，利润12万元．
（Ⅰ）根据题目信息填写下表：
（Ⅱ）设分别生产A、B两种产品x吨、y吨，总产值为z万元，请列出x、y满足的不等式组及目标函数．
（Ⅲ）试问该企业利用现有资源，生产A、B两种产品各多少吨，才能获得最大利润？
（Ⅰ）根据题目信息填写下表：
| 每吨产品 | 煤（吨） | 水（吨） | 电（千瓦） |
| A | |||
| B |
（Ⅲ）试问该企业利用现有资源，生产A、B两种产品各多少吨，才能获得最大利润？
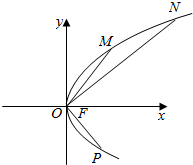已知F是抛物线C：y2=2px（p＞0）的焦点，O为坐标原点．
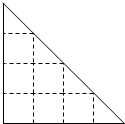网上有一项虚似的游戏，在如图所示的等腰直角三角形上有15个格点（横、纵相邻格点间的距离为1个单位），三角形边界上的每个格点记1分，三角形内部的每个格点记2分，若点击鼠标左键，屏幕上会随机等可能地显示点中的某一格点，点中某格点后，将与其距离为1个单位的格点的分数和作为其得分．
1．将函数f（x）=sin（2x+θ）（-$\frac{π}{2}$＜θ＜$\frac{π}{2}$）的图象向右平移φ（φ＞0）个单位长度后得到函数g（x）的图象，若f（x），g（x）的图象都经过点P（0，$\frac{\sqrt{3}}{2}$），则φ的值可以是（ ）
| A． | $\frac{5π}{3}$ | B． | $\frac{5π}{6}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{6}$ |