题目内容
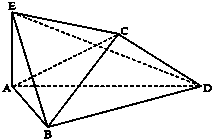菱形ABCD边长为2，∠BAD=60°，将ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，AE⊥平面ABD，且AE=| 3 |
（1）求证：DE⊥AC；
（2）求证：直线BE上是否存在一点M，使得CM∥平面ADE，若存在，求点M的位置，不存在请说明理由．
考点：直线与平面平行的性质
专题：空间位置关系与距离
分析：（1）要证DE⊥AC，只需要证明AC⊥面BDE，即可得到结论；
（2）设M为BE中点，通过面面平行来证线面平行，关键证明面MFC∥面ADE．
（2）设M为BE中点，通过面面平行来证线面平行，关键证明面MFC∥面ADE．
解答：
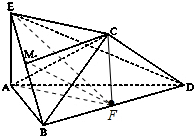证明：（1）设F为BD的中点，连接AF、CF，EF，
∵菱形ABCD边长为2，∠BAD=60°，
∴△ABD，△BCD为正三角形，
∴CF⊥BD，
∵平面ABD⊥平面CBD，
∴CF⊥面ABD，∴CF⊥AF，且CF=
，
∵AE⊥平面ABD，且AE=
，
∴AE=CF，AE∥CF，
即四边形AECF是正方形，则对角线AC⊥EF，
∵ABCD是菱形，∴AF⊥BD，
即BD⊥平面AECF，即BD⊥AC，
∴AC⊥面EFD，
∵DE?面EFD，
∴AC⊥DE；
（2）当M为BE中点，F为BD中点，∴MF∥DE，
又由（1）知，正方形AFCE，
∴CF∥AE，MF、CF?面MFC，MF∩CF=F，AE、ED?面ADE，AE∩ED=E，
∴面MFC∥面ADE，
∵CM?面MFC，∴CM∥平面ADE．
证明：（1）设F为BD的中点，连接AF、CF，EF，∵菱形ABCD边长为2，∠BAD=60°，
∴△ABD，△BCD为正三角形，
∴CF⊥BD，
∵平面ABD⊥平面CBD，
∴CF⊥面ABD，∴CF⊥AF，且CF=
| 3 |
∵AE⊥平面ABD，且AE=
| 3 |
∴AE=CF，AE∥CF，
即四边形AECF是正方形，则对角线AC⊥EF，
∵ABCD是菱形，∴AF⊥BD，
即BD⊥平面AECF，即BD⊥AC，
∴AC⊥面EFD，
∵DE?面EFD，
∴AC⊥DE；
（2）当M为BE中点，F为BD中点，∴MF∥DE，
又由（1）知，正方形AFCE，
∴CF∥AE，MF、CF?面MFC，MF∩CF=F，AE、ED?面ADE，AE∩ED=E，
∴面MFC∥面ADE，
∵CM?面MFC，∴CM∥平面ADE．
点评：本题考查空间直线垂直和线面平行的判定，要求熟练掌握相应的判定定理是解决本题的关键．
练习册系列答案
相关题目
已知f（x）=
，则f[f（-2）]的值为（ ）
|
| A、2 | ||
B、
| ||
| C、-1 | ||
| D、4 |
如图，在直三棱柱ABC-A1B1C1中，AB=1，AC=AA1=