题目内容
15.函数y=3sin(2x-$\frac{π}{3}$)的最小正周期( )| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 3π |
分析 利用函数y=Asin(ωx+φ)的周期为$\frac{2π}{ω}$,可得结论.
解答 解:函数y=3sin(2x-$\frac{π}{3}$)的最小正周期为$\frac{2π}{2}$=π,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的周期性,利用了函数y=Asin(ωx+φ)的周期为$\frac{2π}{ω}$,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
5.某市对贫困家庭自主创业给予小额贷款补贴,每户贷款为2万元,贷款期限有6个月、12个月、18个月、24个月、36个月五种,这五种贷款期限政府分别需要补助200元、300元、300元、400元,从2016年享受此项政策的困难户中抽取了100户进行了调查,选取贷款期限的频数如表:
以上表各种贷款期限频率作为2017年贫困家庭选择各种贷款期限的概率.
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共需要补贴多少万元.
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共需要补贴多少万元.
6.实数x,y满足$\left\{\begin{array}{l}x-2y+2≥0\\ x+y≤1\\ y+1≥0\end{array}\right.$且z=2x-y,则z的最大值为( )
| A. | -7 | B. | -1 | C. | 5 | D. | 7 |
20.直线$x-\sqrt{3}y-1=0$的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
4.若复数z的共轭复数是$\overline{z}$,且满足$\frac{\overline{z}}{1+i}$=i(其中i为虚数单位),则z=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
5.在x∈[4,6],y∈[2,4]内随机取出两个数,则这两个数满足x-y-3>0的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{16}$ |
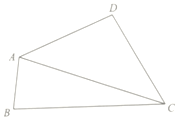 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2,
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2, 如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2
如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2