题目内容
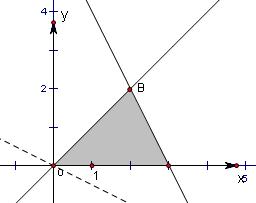
6.设实数x,y满足$\left\{\begin{array}{l}{y≤x}\\{y≥0}\\{y≤-2x+6}\end{array}\right.$,则x+3y的最大值为,8;若x2+4y2≤a恒成立,则实数a为20.分析 先根据约束条件画出可行域,设z=x+3y,再利用z的几何意义求最值,只需求出直线z=x+3y过可行域内的点B时,从而得到z值即可;要求x2+4y2≤a恒成立只要求出x2+4y2的最大值即可,可以令u=x,v=2y,代出x,y满足约束条件$\left\{\begin{array}{l}{2u-v≥0}\\{v≥0}\\{4u+v-12≤0}\end{array}\right.$,根据简单线性规划问题进行求解.
解答 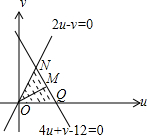
 解:先根据约束条件画出可行域,设z=x+3y,
解:先根据约束条件画出可行域,设z=x+3y,
将最大值转化为y轴上的截距,
由$\left\{\begin{array}{l}{y=x}\\{2x+y-6=0}\end{array}\right.$,得B(2,2).
当直线z=x+3y即$y=-\frac{x}{3}+\frac{z}{3}$经过点B( 2,2)时,z最大,
数形结合,将点B的坐标代入z=x+3y得z最大值为:8;
由x2+4y2≤a可得a≥x2+4y2的最大值,
令x=u,2y=v,则$\left\{\begin{array}{l}{\frac{v}{2}≤u}\\{v≥0}\\{2u+\frac{v}{2}-6≤0}\end{array}\right.$,即$\left\{\begin{array}{l}{2u-v≥0}\\{v≥0}\\{4u+v-12≤0}\end{array}\right.$,
则x2+4y2=u2+v2≥OM2=$(\frac{12}{\sqrt{16+1}})^{2}=\frac{144}{17}$,
又$({u}^{2}+{v}^{2})_{max}=O{N}^{2}=20>O{Q}^{2}=9$,
∴a≥20.
故答案为:8,20.
点评 本题主要考查了简单的线性规划,考查了转化思想和数形结合的思想,以及利用几何意义求最值,解题的关键是会利用换元法进行求解,是中档题.

| A. | 3 | B. | $\frac{9}{5}$ | C. | 6 | D. | 1 |
| A. | 2+6i | B. | 2-4i | C. | -2+6i | D. | -3-6i |