题目内容
已知命题p:?m∈[-1,1],不等式a2-5a-3≤
,命题q:?x∈R,使不等式x2+ax+2<0.若“p或q”是真命题,?p是真命题,求a的取值范围.
| m2+9 |
考点:复合命题的真假
专题:简易逻辑
分析:由已知得出0≤
≤
根据?m∈[-1,1],不等式a2-5a-3≤
,只需a2-5a-3≤0;先求出x2+ax+2≥0对x∈R恒成立时a的范围,再求出其补集;根据“p或q”是真命题,?p是真命题得出p为假命题q为真命题
| m2+9 |
| 10 |
| m2+9 |
解答:
解:若命题是真命题
∵m∈[-1,1],
∴3≤
≤
∵?m∈[-1,1],不等式a2-5a-3≤
∴a2-5a-3≤3,
即a2-5a-6≤0
解得-1≤a≤6,
若命题q为真命题
∵x2+ax+2≥0对x∈R恒成立时
∴△=a2-8≤0
解得-2
≤a≤2
∵?x∈R,使不等式x2+ax+2<0
∴a<-2
或a>2
“p或q”是真命题,?p是真命题
p为假命题q为真命题,
即
,
∴a>6或a<-2
.
∵m∈[-1,1],
∴3≤
| m2+9 |
| 10 |
∵?m∈[-1,1],不等式a2-5a-3≤
| m2+9 |
∴a2-5a-3≤3,
即a2-5a-6≤0
解得-1≤a≤6,
若命题q为真命题
∵x2+ax+2≥0对x∈R恒成立时
∴△=a2-8≤0
解得-2
| 2 |
| 2 |
∵?x∈R,使不等式x2+ax+2<0
∴a<-2
| 2 |
| 2 |
“p或q”是真命题,?p是真命题
p为假命题q为真命题,
即
|
∴a>6或a<-2
| 2 |
点评:本题主要考考查了复合命题的真假判定的应用,解题的关键是根据已知条件分别求解p,q为真时的范围.

练习册系列答案
相关题目
 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.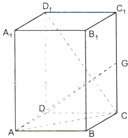 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,G是CC1上的动点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,G是CC1上的动点.