题目内容
4.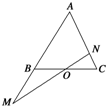 如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$ (m,n>0),则m2+n的范围为[$\frac{7}{4}$,4).
如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$ (m,n>0),则m2+n的范围为[$\frac{7}{4}$,4).
分析 用$\overrightarrow{AM},\overrightarrow{AN}$表示出$\overrightarrow{AO}$,根据M,O,N三点共线得出m,n的关系,从而得出m2+n关于m的二次函数,求出m的范围,利用二次函数的性质求出范围.
解答 解:∵O是BC的中点,∴$\overrightarrow{AO}$=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$=$\frac{m}{2}\overrightarrow{AM}+\frac{n}{2}\overrightarrow{AN}$,
∵M,O,N三点共线,
∴$\frac{m}{2}+\frac{n}{2}=1$,即n=2-m.
∴m2+n=m2-m+2=(m-$\frac{1}{2}$)2+$\frac{7}{4}$,
∵m>0,n>0,即$\left\{\begin{array}{l}{m>0}\\{2-m>0}\end{array}\right.$,
∴0<m<2.
令f(m)=(m-$\frac{1}{2}$)2+$\frac{7}{4}$,
∴当m=$\frac{1}{2}$时,f(m)取得最小值$\frac{7}{4}$,
当m=2时,f(m)取得最大值4.
∴$\frac{7}{4}≤f(m)<4$.
故答案为:$[{\frac{7}{4},4})$.
点评 本题考查了平面向量的基本定理,二次函数的性质,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
12.已知f(x)是定义在R上的可导函数,当x∈(1,+∞)时,(x-1)f′(x)-f(x)>0恒成立,若a=f(2),b=$\frac{1}{2}$f(3),c=$\frac{1}{{\sqrt{2}-1}}f(\sqrt{2})$,则a,b,c的大小关系是( )
| A. | c<a<b | B. | a<b<c | C. | b<a<c | D. | a<c<b |
19.已知f(x)=asin2x-$\frac{1}{3}$sin3x(a为常数),在x=$\frac{π}{3}$处取得极值,则a=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{2}{3}$ | D. | $-\frac{1}{2}$ |
13.函数f(x)=(x-3)ex的单调增区间是( )
| A. | (-∞,2) | B. | (2,+∞) | C. | (1,4) | D. | (0,3) |
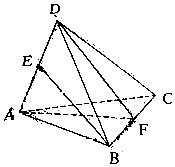 如图,在空间四边形ABCD中,AB,BC,CD,DA的长和两条对角线AC,BD都相等,且E为AD的中点,F为BC的中点,则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$.
如图,在空间四边形ABCD中,AB,BC,CD,DA的长和两条对角线AC,BD都相等,且E为AD的中点,F为BC的中点,则直线BE和平面ADF所成的角的正弦值为$\frac{\sqrt{3}}{3}$.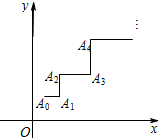 一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图,A0(x0,y0)的坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.
一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图,A0(x0,y0)的坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.