题目内容
已知函数f(x)=x2-(a-1)x-b-1,当x∈[b, a]时,函数f(x)的图像关于y轴对称,数列{an}的前n项和为Sn,且Sn=f(n).
(1)求数列{an}的通项公式;
(2)设bn= , Tn=b1+b2+…+bn,若Tn>2m,求m的取值范围。
, Tn=b1+b2+…+bn,若Tn>2m,求m的取值范围。
解:(1)x∈[b, a]时,函数f(x)的图像关于y轴对称,可知f(-x)=f(x),a+b=0,即(a-1)x=0对任意x都成立,得a=1,b=-1
由Sn=f(n)= n2,得
n=1时a1=1

故
(2)bn=



可得

由 ,可知
,可知
由Tn>2m,可得 ,解得
,解得

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1, 2)在“上”区域内,则双曲线离心率的取值范围为 。
的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1, 2)在“上”区域内,则双曲线离心率的取值范围为 。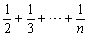 (n∈N*),经计算得f(4)>2, f(8)>
(n∈N*),经计算得f(4)>2, f(8)>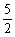 , f(16)>3, f(32)>
, f(16)>3, f(32)> ,
, A.54cm2
A.54cm2  cm2
cm2  的左顶点A且斜率为k的直线交椭圆C于另一个点B,且点B在x轴上的射影恰好为右焦点F,若
的左顶点A且斜率为k的直线交椭圆C于另一个点B,且点B在x轴上的射影恰好为右焦点F,若 <k<
<k< , 则椭圆的离心率的取值范围是 。
, 则椭圆的离心率的取值范围是 。 命题
命题 :“
:“ 中,若
中,若 则
则 。则下列命题为真命题的是 ( )
。则下列命题为真命题的是 ( ) B.
B. C.
C. D.
D.
 上的非负可导函数f(x)满足xf′(x)
上的非负可导函数f(x)满足xf′(x) ,对任意正数
,对任意正数 ,若满足
,若满足 ,则必有( )
,则必有( ) B.
B. C.
C. D.
D.
 =
=  的最大值为( )
的最大值为( ) B.
B.  C. e D.
C. e D. 