题目内容
2. 在长方体ABCD-A1B1C1D1中,AA1=6,AB=3,AD=8,点M是棱AD的中点,N在棱AA1上,且满足AN=2NA1,P是侧面四边形ADD1A1内一动点(含边界),若C1P∥平面CMN,则线段C1P长度最小值是( )
在长方体ABCD-A1B1C1D1中,AA1=6,AB=3,AD=8,点M是棱AD的中点,N在棱AA1上,且满足AN=2NA1,P是侧面四边形ADD1A1内一动点(含边界),若C1P∥平面CMN,则线段C1P长度最小值是( )| A. | $\sqrt{17}$ | B. | 4 | C. | $\sqrt{15}$ | D. | 3 |
分析 取A1D1中点E,在DD1上取点F,使D1F=2DF,连结EF、C1E、C1F,则平面CMN∥平面C1EF,由此推导出P∈线段EF,当P与EF的中点O重合时,线段C1P长度取最小值PO,当P与点E或点F重合时,线段C1P长度取最大值PE或PF,由此能求出线段C1P的最小值.
解答 解: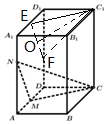 取A1D1中点E,在DD1上取点F,使D1F=2DF,连结EF、C1E、C1F,
取A1D1中点E,在DD1上取点F,使D1F=2DF,连结EF、C1E、C1F,
则平面CMN∥平面C1EF,
∵是侧面四边形ADD1A1内一动点(含边界),C1P∥平面CMN,
∴P∈线段EF,
∴当P与EF的中点O重合时,线段C1P长度取最小值PO,
当P与点E或点F重合时,线段C1P长度取最大值PE或PF,
∵在长方体ABCD-A1B1C1D1中,AA1=6,AB=3,AD=8,
点M是棱AD的中点,点N在棱AA1上,且满足AN=2NA1,
∴C1Pmax=C1E=C1F=$\sqrt{{3}^{2}+{4}^{2}}$=5,EF=4$\sqrt{2}$,
C1Pmin=PO=$\sqrt{{C}_{1}{E}^{2}-E{O}^{2}}$=$\sqrt{25-(2\sqrt{2})^{2}}=\sqrt{17}$.
∴线段C1P长度的最小值为$\sqrt{17}$.
故选:A.
点评 本题考查线段的最小值的求法,突出对运算能力、化归转化能力、空间想象的考查,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若数列{an}满足a1+2a2+3a3+…+nan=n2(n∈N*),则a7=( )
| A. | $\frac{9}{5}$ | B. | $\frac{11}{6}$ | C. | $\frac{13}{7}$ | D. | 2 |
11.要得到函数f(x)=cos(2x-$\frac{π}{3}$)+1的图象,只需把y=2cos2x的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向上平移1个单位 | D. | 向上平移2个单位 |
 已知函数$f(x)=3sin(\frac{x}{2}+\frac{π}{6})+3$
已知函数$f(x)=3sin(\frac{x}{2}+\frac{π}{6})+3$