题目内容
若函数y=x2+|x-a|+b在区间(-∞,0]上为减函数,则a的取值范围是 .
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:结合区间(-∞,0],对a进行讨论,从而去掉绝对值号,讨论单调性,解出a的取值范围.
解答:
解:y=x2+|x-a|+b=
,
①当a≥0时,在区间(-∞,0]上,
y=x2+|x-a|+b=x2-x+a+b,
此时符合题意.
②当a<0时,在区间(-∞,0]上,
y═
,
则在[a,0]或[-
,0]上一定为增函数;
故不符合题意.
综上所述,a≥0.
故答案为:a≥0.
|
①当a≥0时,在区间(-∞,0]上,
y=x2+|x-a|+b=x2-x+a+b,
此时符合题意.
②当a<0时,在区间(-∞,0]上,
y═
|
则在[a,0]或[-
| 1 |
| 2 |
故不符合题意.
综上所述,a≥0.
故答案为:a≥0.
点评:本题考查了二次函数的单调性,注意去绝对值的方法.同时考查了分类讨论的思想.

练习册系列答案
相关题目
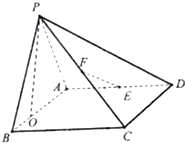 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD,PC的中点
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD,PC的中点 如图程序框图是计算22+42+…++1 0002的值,程序框图中条件语句中应填写
如图程序框图是计算22+42+…++1 0002的值,程序框图中条件语句中应填写