题目内容

已知F是椭圆C：+=1（a＞b＞0）的右焦点，点P在椭圆C上，且线段PF与圆（其中c2=a2-b2）相切于点Q，且=2，则椭圆C的离心率等于（ ）

A．
B．
C．
D．
【答案】分析：设椭圆的左焦点为F1，确定PF1⊥PF，，|PF1|=b，|PF|=2a-b，即可求得椭圆的离心率．
解答：解：设椭圆的左焦点为F1，连接F1，设圆心为C，则
∵
∴圆心坐标为，半径为r=
∴|F1F|=3|FC|
∵=2，
∴PF1∥QC，|PF1|=b
∴|PF|=2a-b
∵线段PF与圆（其中c2=a2-b2）相切于点Q，
∴CQ⊥PF
∴PF1⊥PF
∴b2+（2a-b）2=4c2
∴b2+（2a-b）2=4（a2-b2）
∴
∴
∴
故选A．
点评：本题考查椭圆的几何性质，考查直线与圆的位置关系，确定几何量的关系是关键．
练习册系列答案
相关题目
已知F是椭圆C的一个焦点，B是短轴的一个端点，线段BF的延长线交C于点D，且
BF
=2
FD
，则C的离心率为
 
．
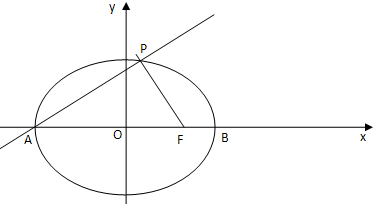精英家教网已知椭圆C的方程是
x2
a2
+
y2
b2
=1（a＞b＞0），点A，B分别是椭圆的长轴的左、右端点，
左焦点坐标为（-4，0），且过点P ( 
3
2
，  
5
2
3
)．
（Ⅰ）求椭圆C的方程；
（Ⅱ）已知F是椭圆C的右焦点，以AF为直径的圆记为圆M，试问：过P点能否引圆M的切线，若能，求出这条切线与x轴及圆M的弦PF所对的劣弧围成的图形的面积；若不能，说明理由．
已知F是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点，点P在椭圆C上，线段PF与圆x2+y2=b2相切于点Q，且
PQ
=
QF
，则椭圆C的离心率为
5
3
5
3
．
已知F是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点，点P在椭圆C上，且线段PF与圆(x-
c
3
)2+y2=
b2
9
（其中c2=a2-b2）相切于点Q，且
PQ
=2
QF
，则椭圆C的离心率等于（　　）
已知F是椭圆C：
x2
16
+
y2
7
=1的左焦点，过原点O的直线交椭圆C于P，Q两点，若|PF|•|QF|=9，则|PQ|=
2
14
2
14
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网