题目内容
8.已知两圆x2+y2=10和(x-1)2+(y-3)2=20相交于A,B两点,则公共弦AB的长度等于( )| A. | 2$\sqrt{10}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{5}$ | D. | 4 |
分析 当判断出两圆相交时,直接将两个圆方程作差,即得两圆的公共弦所在的直线方程.圆心(0,0)在直线上,可得公共弦AB的长度.
解答 解:因为两圆相交于A,B两点,
则A,B两点的坐标坐标既满足第一个圆的方程,又满足第二个圆的方程
将两个圆方程作差,得直线AB的方程是:x+3y=0,
圆心(0,0)在直线上,所以公共弦AB的长度等于2$\sqrt{10}$,
故选:A.
点评 本题考查圆与圆的位置关系,考查直线与圆的位置关系,考查学生的计算能力,比较基础.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
19.某公司准备投入适当的广告费对其生产的产品进行促销,在一年内,根据预算得某产品的年利润S(万元)与广告费x(万元)之间的函数解析式为S=25-($\frac{x}{4}$+$\frac{16}{x}$)(x>0),则当该公司的年利润最大时应投人广告费( )
| A. | 9万元 | B. | 8万元 | C. | 7万元 | D. | 6万元 |
13.函数f(x)=(6x-$\frac{3}{2}$)2tan(4x-1)+x+$\frac{3}{4}$,f($\frac{1}{2n}$)+f($\frac{1}{n}$)+f($\frac{3}{2n}$)+…+f($\frac{n-1}{2n}$)=( )
| A. | n | B. | n-1 | C. | $\frac{n}{2}$ | D. | $\frac{n-1}{2}$ |
17.把三张不同的游园票分给10个人中的3人,分法有( )
| A. | A${\;}_{10}^{3}$种 | B. | C${\;}_{10}^{3}$ 种 | ||
| C. | C${\;}_{10}^{3}$A${\;}_{10}^{3}$种 | D. | 30 种 |
18.“c=6”是“函数f(x)=x(x-c)2在x=2处有极大值”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
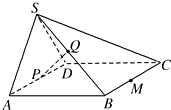 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.