题目内容
9.极坐标方程ρ=2sin($\frac{π}{3}$+θ)化为直角坐标方程为( )| A. | (x-$\frac{{\sqrt{3}}}{2}$)2+(y-$\frac{1}{2}$)2=1 | B. | y=2(x-$\frac{3}{2}$) | C. | (x-$\frac{{\sqrt{3}}}{2}$)(y-$\frac{1}{2}$)=1 | D. | 4x2+12y2=1 |
分析 利用两角和的正弦函数化简方程,然后转化为普通方程.
解答 解:ρ=2sin($\frac{π}{3}$+θ)=$\sqrt{3}$cosθ+sinθ,
即ρ2=$\sqrt{3}$ρcosθ+ρsinθ,
可得x2+y2=$\sqrt{3}x$+y.
即:(x-$\frac{{\sqrt{3}}}{2}$)2+(y-$\frac{1}{2}$)2=1.
故选:A.
点评 本题考查简单曲线的极坐标方程与普通方程的互化,基本知识的考查.

练习册系列答案
相关题目
17.已知偶函数f(x)在[0,π]上单调递增,那么下列各式正确的是( )
| A. | f(-π)>f(log2$\frac{1}{4}$)>f($-\frac{π}{2}$) | B. | f(log2$\frac{1}{4}$)>f(-$\frac{π}{2}$)>f(-π) | ||
| C. | f(-π)>f(-$\frac{π}{2}$)>f(log2$\frac{1}{4}$) | D. | f(-$\frac{π}{2}$)>f(log2$\frac{1}{4}$)>f(-π) |
14.如图(算法流程图)的输出值x为( )


| A. | 13 | B. | 12 | C. | 22 | D. | 11 |
1.直线l的参数方程是$\left\{\begin{array}{l}{x=1+2t}\\{y=2-t}\end{array}\right.$(t∈R),则l的斜率为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | 2 |
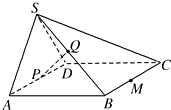 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD,四边形ABCD为正方形,且P为AD的中点,Q为SB的中点.