题目内容
15．若直线l：ax+by+4=0（a＞0，b＞0）始终平分圆x2+y2+8x+2y+1=0，则ab的最大值为1．分析 由题意可得直线经过圆的圆心（-4，-1），4a+b=4，再利用基本不等式求得ab的最大值．
解答 解：∵直线ax+by+4=0（a＞0，b＞0）始终平分圆x2+y2+8x+2y+1=0，
∴直线经过圆的圆心（-4，-1），
则有-4a-b+4=0，即 4a+b=4，
由基本不等式可得，4a+b=4≥2$\sqrt{4ab}$=4$\sqrt{ab}$，
当且仅当2a=b=$\frac{1}{2}$时，取等号，由此可得ab≤1，
∴ab的最大值是1，
故答案为：1．
点评 本题主要考查了直线和圆相交的性质，基本不等式的应用，解题的关键是直线平分圆的性质的应用，属于中档题．
练习册系列答案
相关题目
5．下列说法正确的是（ ）
| A． | 图象连续的函数f（x）在区间（a，b）上一定存在最值 | |
| B． | 函数的极小值可能大于极大值 | |
| C． | 函数的最小值一定是极小值 | |
| D． | 函数的极小值一定是最小值 |
3．
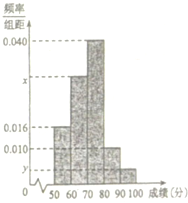某中学举行了一次“环保知识竞赛”活动，为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出如图所示的频率分布直方图，但由于不慎丢失了部分数据．已知得分在[50，60）的有8人，在[90，100）的有2人，由此推测频率分布直方图中的x=（ ）
某中学举行了一次“环保知识竞赛”活动，为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出如图所示的频率分布直方图，但由于不慎丢失了部分数据．已知得分在[50，60）的有8人，在[90，100）的有2人，由此推测频率分布直方图中的x=（ ）| A． | 0.04 | B． | 0.03 | C． | 0.02 | D． | 0.01 |
10．若S1=${∫}_{0}^{1}$（ex-1）dx，S2=${∫}_{0}^{1}$xdx，S3=${∫}_{0}^{1}$sinxdx，则（ ）
| A． | S2＞S3＞S1 | B． | S1＞S3＞S2 | C． | S2＞S1＞S3 | D． | S1＞S2＞S3 |
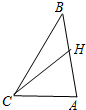如图，在△ABC中，已知CA=2，CB=3，∠ACB=60°．