题目内容
已知函数f(x)＝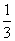
ax3－
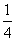x2＋cx＋d(a，c，d∈R)满足f(0)＝0，f′(1)＝0，且f′(x)≥0在R上恒成立．
(1)求a，c，d的值；
(2)若h(x)＝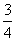
x2－bx＋
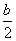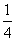－，解不等式f′(x)＋h(x)<0；
(3)是否存在实数m，使函数g(x)＝f′(x)－mx在区间[m，m＋2]上有最小值－5？若存在，求出实数m的值；若不存在，请说明理由．
∵f′(x)≥0在R上恒成立，即ax2－
x＋c≥0恒成立，
∵
>－1，∴m＝舍去，故m＝－3.
练习册系列答案
阅读快车系列答案
相关题目
B(2，0)，点C、D满足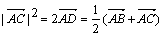
离为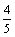
，且l与D的轨迹相切，求椭圆方程．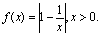 
D．2
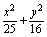=1相交于A、B两点，l又与双曲线x2-y2=1相交于C、D两点，C、D三等分线段AB，求直线l的方程 
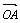与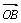
夹角的大小；
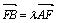，若λ∈[4，9]，求l在y轴上截距的变化范围．
＋
＋
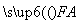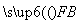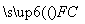＝0，且|