题目内容
9.已知函数f(x)=x3+ax2+bx+c在$x=-\frac{2}{3}$与x=1处都取得极值.(1)求a,b的值;
(2)若对x∈R,f(x)有三个零点,求实数c的取值范围.
分析 (1)求出函数导数,得到关于a,b的方程组,解出即可;
(2)求出函数的导数,解关于导函数的不等式,求出函数的极值,根据函数的零点的个数得到关于c的不等式组,解出即可.
解答 解:(1)∵f'(x)=3x2+2ax+b
由已知有 $\left\{\begin{array}{l}{f′(-\frac{2}{3})=0}\\{f′(1)=0}\end{array}\right.$,解得a=-$\frac{1}{2}$,b=-2;
(2)由(1)得:f(x)=x3-$\frac{1}{2}$x2-2x+c,
f′(x)=由f'(x)>0得x>1或x<-$\frac{2}{3}$,
由f'(x)<0得-$\frac{2}{3}$<x<1,
故当x=-$\frac{2}{3}$时,f(x)有极大值c+$\frac{22}{27}$,
当x=1时,f(x)有极小值c-$\frac{3}{2}$,
若对x∈R,f(x)有三个零点,
则$\left\{\begin{array}{l}{c+\frac{22}{27}>0}\\{c-\frac{3}{2}<0}\end{array}\right.$,解得:-$\frac{22}{27}$<c<$\frac{3}{2}$.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
相关题目
20.某几何体的三视图如图所示,已知三视图中的圆的半径均为2,则该几何体的体积为( )

| A. | $\frac{20π}{3}$ | B. | 12π | C. | $\frac{44π}{3}$ | D. | 16π |
14.已知集合M={x|lnx>0},N={x|x2-3x-4>0},则M∩N=( )
| A. | (-1,4) | B. | (1,+∞) | C. | (1,4) | D. | (4,+∞) |
1.F是抛物线y2=2x的焦点,以F为端点的射线与抛物线相交于A,与抛物线的准线相交于B,若$\overrightarrow{FB}=4\overrightarrow{FA}$,则$\overrightarrow{FA}•\overrightarrow{FB}$=( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{9}{4}$ |
17.若的(x2+a)(x-$\frac{1}{x}$)10展开式中x6的系数为-30,则常数a=( )
| A. | -4 | B. | -3 | C. | 2 | D. | 3 |
16.如图,某几何体的三视图如图所示,则该几何体的各条棱中最长的棱和最短的棱长度之和为( )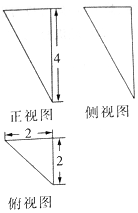

| A. | 6 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{5}$+2 | D. | 2$\sqrt{6}$+2 |