题目内容
12.在△ABC中,角A,B,C的对边分别为a,b,c,若b(tanA+tanB)=$\sqrt{2}$ctanB,BC边的中线长为1,则a的最小值为2$\sqrt{2}$-2.分析 利用正弦定理化简条件式可得cosA=$\frac{\sqrt{2}}{2}$,由向量线性运算的几何意义可得$|\overrightarrow{AB}+\overrightarrow{AC}|$=2,两边平方得出b,c间的关系,使用基本不等式解出bc的范围,于是a=|$\overrightarrow{AB}-\overrightarrow{AC}$|,两边平方即可求出a2的最小值.
解答 解:在△ABC中,∵b(tanA+tanB)=$\sqrt{2}$ctanB,∴b($\frac{sinA}{cosA}+\frac{sinB}{cosB}$)=$\sqrt{2}c$$\frac{sinB}{cosB}$,
∴bsinC=$\sqrt{2}$csinBcosA,
∴bc=$\sqrt{2}$bccosA,∴cosA=$\frac{\sqrt{2}}{2}$.
∵BC边的中线长为1,∴$|\overrightarrow{AB}+\overrightarrow{AC}|$=2,
∴c2+b2+2bccosA=4,即b2+c2=4-$\sqrt{2}$bc≥2bc,解得bc≤4-2$\sqrt{2}$.
∴a2=($\overrightarrow{AB}-\overrightarrow{AC}$)2=b2+c2-2bccosA=4-2$\sqrt{2}$bc≥4-2$\sqrt{2}$(4-2$\sqrt{2}$)=12-8$\sqrt{2}$.
∴a的最小值为$\sqrt{12-8\sqrt{2}}$=2$\sqrt{2}$-2.
故答案为:2$\sqrt{2}-2$.
点评 本题考查了正弦定理,向量在几何中的应用,基本不等式的应用,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
2.i为虚数单位,则复数$\frac{3-2i}{i}$=( )
| A. | 2-3i | B. | -2-3i | C. | 3-2i | D. | -2+3i |
3.“a>2且b>2”是“ab>4”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.已知x,y满足线性约束条件$\left\{\begin{array}{l}x-2y≤0\\ x+y-4≤0\\ 2x+y-4≥0\end{array}$,则目标函数z=$\frac{x+1}{y+2}$的最小值为( )
| A. | $\frac{1}{6}$ | B. | $\frac{11}{10}$ | C. | $\frac{13}{14}$ | D. | $\frac{10}{11}$ |
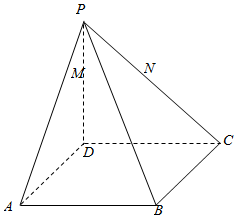 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,M,N分别为PD,PC上的点,且$\frac{PM}{MD}$=$\frac{PN}{NC}$,求证:MN∥AB.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,M,N分别为PD,PC上的点,且$\frac{PM}{MD}$=$\frac{PN}{NC}$,求证:MN∥AB.