题目内容
已知函数f（x）=x2+丨x-a丨，a为常数．设a＞0，g（x）=
，x∈（0，a]为减函数，求实数a的取值范围．
| f(x) |
| x |
考点：函数单调性的性质
专题：函数的性质及应用
分析：由题意可得x∈（0，a]，g（x）=x+
-1为减函数，g′（x）≤0 恒成立，即1-
≤0，由此求得实数a的取值范围．
| a |
| x |
| a |
| a2 |
解答：
解：由题意可得a＞0，x∈（0，a]，g（x）=
=x+
=x+|1-
|=x+
-1 为减函数．
∴g′（x）=1-
≤0 恒成立，∴1-
≤0，解得0＜a≤1，
故a的范围是（0，1]．
| f(x) |
| x |
| |x-a| |
| x |
| a |
| x |
| a |
| x |
∴g′（x）=1-
| a |
| x2 |
| a |
| a2 |
故a的范围是（0，1]．
点评：本题主要考查函数的单调性的性质，函数的恒成立问题，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
已知等比数列{an}中，a1a2a3a4a5=32，且a11=8，则a7的值为（ ）
| A、4 | ||
| B、-4 | ||
| C、±4 | ||
D、±2
|
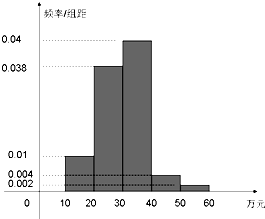在某市的人大贿选案中，经调查统计该市人大代表的受贿情况的频率分布直方图如图：其中受贿[10，20]万元的有10人．