题目内容
7．用硬纸依据如图所示（单位；cm）的平面图形制作一个几何体，画出该几何体的三视图并求出其表面
分析 由题目给出的平面图形，可得几何体为圆锥加底座圆柱的形式，画出直观图，可得三视图，把三个平面图形面积作和求得几何体的表面积．
解答 
解：如图，∵所给优弧长度为2π×4×$\frac{3}{4}$=6π=圆形周长为2π×3=6π≈19
∴几何体为圆锥加底座圆柱的形式，
则几何体表面积为三个平面图形面积之和，
即S=S矩形+S扇形+S圆=（1×19）+$\frac{3}{4}$×16π+9π=19+12π+9π，
∵题干默认6π=19，
∴S=19+38+28.5=85.5．
即几何体表面积为85
点评 本题考查柱、锥、台体的体积，考查空间想象能力和思维能力，是中档题．
练习册系列答案
相关题目
15．某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究，他们分别记录了3月1日至3月5月的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数，得到如表资料：
（1）从3月1日至3月5日中任选2天，记发芽的种子数分别为m，n，求事件“m，n均不小于25”的概率
（2）请根据3月2日至3月4日的三组数据，求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（3）若由线性回归方程得到的估计数据与所需要检验的数据误差均不超过2颗，则认为得到的线性回归方程是可靠的，试用3月1日与3月5日的两组数据检验，问（2）中所得的线性回归方程是否可靠？
（参考公式：$\widehatb=\frac{{\sum_{i=1}^{i=n}{（{{x_i}-\overline x}）•（{{y_i}-\overline y}）}}}{{\sum_{i=1}^{i=n}{{{（{{x_i}-\overline x}）}^2}}}}$或$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-b$\overline{x}$）
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 昼夜温差（．C） | 10 | 11 | 13 | 12 | 8 |
| 发芽数（颗） | 23 | 25 | 30 | 26 | 16 |
（2）请根据3月2日至3月4日的三组数据，求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
（3）若由线性回归方程得到的估计数据与所需要检验的数据误差均不超过2颗，则认为得到的线性回归方程是可靠的，试用3月1日与3月5日的两组数据检验，问（2）中所得的线性回归方程是否可靠？
（参考公式：$\widehatb=\frac{{\sum_{i=1}^{i=n}{（{{x_i}-\overline x}）•（{{y_i}-\overline y}）}}}{{\sum_{i=1}^{i=n}{{{（{{x_i}-\overline x}）}^2}}}}$或$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-b$\overline{x}$）
12．设全集U=R，已知集合A={-2，-1，0，1，2，3}，B={x|$\frac{3}{x-1}$+1≥0}，则集合A∩∁UB=（ ）
| A． | {-1，0，1} | B． | {-1，0} | C． | {-2，-1，0，1} | D． | {-1，0，1，2} |
如图，在四棱锥S-ABCD中，侧棱SA⊥底面ABCD，且底面ABCD是边长为1的正方形，侧棱SA=4，AC与BD相交于点O．
16．若cos（${\frac{π}{6}$-α）=$\frac{1}{3}$，则cos（$\frac{2π}{3}$+2α）=（ ）
| A． | $\frac{2}{9}$ | B． | $-\frac{2}{9}$ | C． | $\frac{7}{9}$ | D． | $-\frac{7}{9}$ |
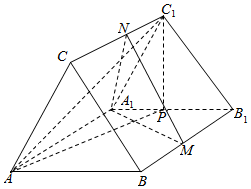如图，直三棱柱ABC-A1B1C1中，△ABC是正三角形，AB=AA1，M是BB1的中点，P是A1B1的中点，N是线段CC1上的动点．