题目内容
18.用分析法证明:设a,b为实数,求证$\sqrt{{a}^{2}+{b}^{2}}$≥$\frac{\sqrt{2}}{2}$(a+b)分析 分析法证明不等式,寻找使$\sqrt{{a}^{2}+{b}^{2}}$≥$\frac{\sqrt{2}}{2}$(a+b)成立的充分条件,直到使不等式成立的条件显然具备为止.
解答 证明:要证$\sqrt{{a}^{2}+{b}^{2}}$≥$\frac{\sqrt{2}}{2}$(a+b),
a+b≤0,显然成立,
a+b>0时,只要证a2+b2≥$\frac{1}{2}$(a+b)2,
只要证2(a2+b2)≥a2+2ab+b2,
只要证(a-b)2≥0,
显然成立,故要证的不等式成立.
点评 本题考查不等式的证明,着重考查分析法的应用,考查推理能力,体现了转化的数学思想,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
8.已知双曲线C的焦点为F1,F2,点P是双曲线上任意一点,若双曲线的离心率为2,且|PF1|=2|PF2|,则cos∠PF2F1=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
8.如果a<b<0,那么下面一定成立的是( )
| A. | ac<bc | B. | a-b>0 | C. | a2>b2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
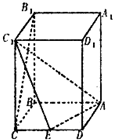 已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,
已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,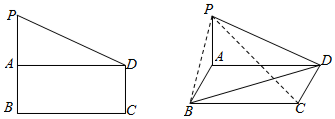 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ:
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,PB=BC=2CD=2,点A是PB的中点,现沿AD将平面PAD折起,设∠PAB=θ: