题目内容
17.设双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一个顶点为(1,0),它的一个焦点与抛物线y2=8x的焦点相同,则双曲线C的方程为x2-$\frac{{y}^{2}}{3}$=1,离心率为2.分析 由题意可得a=1,求得抛物线的焦点(2,0),即有c=2,由a,b,c的关系可得b,进而得到双曲线的方程,由离心率公式计算即可得到所求值.
解答 解:由题意可得a=1,
抛物线y2=8x的焦点为(2,0),
可得c=2,b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$,
即有双曲线的方程为x2-$\frac{{y}^{2}}{3}$=1,
离心率e=$\frac{c}{a}$=2.
故答案为:x2-$\frac{{y}^{2}}{3}$=1,2.
点评 本题考查双曲线的方程的求法和离心率,注意运用双曲线的性质和抛物线的焦点,考查运算能力,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
10.若甲、乙、丙三人中,任选两人参加某项活动,甲被选中的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
8.已知双曲线C的焦点为F1,F2,点P是双曲线上任意一点,若双曲线的离心率为2,且|PF1|=2|PF2|,则cos∠PF2F1=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
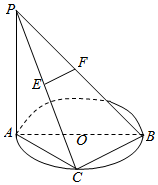 如图,已知PA垂直圆O所在的平面,AB是圆O的直径,AB=2,C是圆O上一点,且PA=AC=BC,E,F分别为PC,PB中点.
如图,已知PA垂直圆O所在的平面,AB是圆O的直径,AB=2,C是圆O上一点,且PA=AC=BC,E,F分别为PC,PB中点.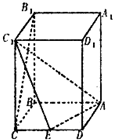 已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,
已知四棱柱ABCD-A1B1C1D1,底面ABCD为菱形,∠ADC=60°,BB1⊥底面ABCD,AA1=AC=4,E是CD的中点,