题目内容
17.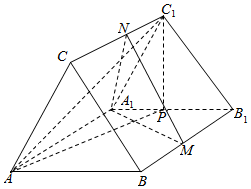 如图,直三棱柱ABC-A1B1C1中,△ABC是正三角形,AB=AA1,M是BB1的中点,P是A1B1的中点,N是线段CC1上的动点.
如图,直三棱柱ABC-A1B1C1中,△ABC是正三角形,AB=AA1,M是BB1的中点,P是A1B1的中点,N是线段CC1上的动点.(Ⅰ)证明:平面APC1⊥平面A1MN;
(Ⅱ)若二面角N-A1M-A的余弦值为$\frac{1}{4}$,求$\frac{CN}{N{C}_{1}}$的值.
分析 (I)根据面面垂直的判定定理证明A1M⊥平面APC1即可
(Ⅱ)建立空间坐标系,利用向量法求出平面的法向量,利用向量法结合二面角的余弦值求出N的位置即可得到结论.
解答 (Ⅰ)证明:∵△A1B1C1是正三角形,P是A1B1的中点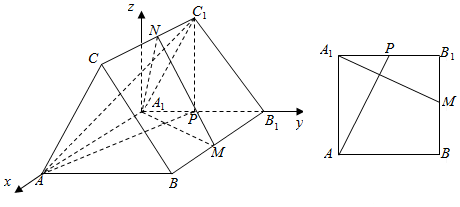
∴C1P⊥A1B1,
则C1P⊥平面ABB1A1,
则C1P⊥A1M,
在正方形ABB1A1,中,M是BB1的中点,
∴C1P⊥AP,
∵AP与A1M相交,
∴A1M⊥平面APC1,
∵A1M?平面A1MN;
∴平面APC1⊥平面A1MN;
(Ⅱ)建立以A1为坐标原点,A1A,A1B1,分别为x,y轴,垂直于平面ABB1A1,的直线为z轴的空间直角坐标系如图:
∵△ABC是正三角形,AB=AA1,
∴设AB=AA1=2,
则A(2,0,0),B(2,2,0),M(1,2,0),C1(0,1,$\sqrt{3}$),
设N(a,1,$\sqrt{3}$),0<a<2,
则平面A1MA的法向量为$\overrightarrow{m}$=(0,0,1),
设平面NA1M的法向量$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{{A}_{1}M}$=(1,2,0),$\overrightarrow{{A}_{1}N}$=(a,1,$\sqrt{3}$),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}M}=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}N}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{x+2y=0}\\{ax+y+\sqrt{3}z=0}\end{array}\right.$,
令y=1,则x=-2,z=$\frac{2a-1}{\sqrt{3}}$,
则$\overrightarrow{n}$=(-2,1,$\frac{2a-1}{\sqrt{3}}$),
若二面角N-A1M-A的余弦值为$\frac{1}{4}$,
则|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$|=$\frac{|\frac{2a-1}{\sqrt{3}}|}{\sqrt{4+1+\frac{(2a-1)^{2}}{3}}}$=$\frac{1}{4}$,
整理得(2a-1)2=1,得2a-1=1或2a-1=-1,
得a=1或a=0(舍),
即N是CC1的中点,
则$\frac{CN}{N{C}_{1}}$=1.
点评 本题主要考查面面垂直判定以及二面角的求解,建立空间直角坐标系,利用向量法进行求解,综合性较强,运算量较大.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案| A. | ac<bc | B. | a-b>0 | C. | a2>b2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
| A. | $\frac{1}{2}n(n+1)$ | B. | $\frac{1}{2}n(3n-1)$ | C. | n2-n+1 | D. | n2-2n+2 |
| A. | $\frac{2\sqrt{2}}{9}$ | B. | $\frac{2\sqrt{3}}{9}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
