Question

已知抛物线y²=6x上的两个动点A（x₁，y₁）和B（x₂，y₂），其中x₁≠x₂且x₁+x₂=4．线段AB的垂直平分线与x轴交于点C．
（1）试证直线AB的垂直平分线经过定点．
（2）设AB中点为M（x₀，y₀），求△ABC面积的表达式，要求用y₀表示．
（3）求△ABC面积的最大值．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）设线段AB的中点为M（x₀，y₀），则kAB=

y2-y1

x2-x1

=

y2-y1

y 2 2 6 - y 2 1 6

=

6

y2+y1

=

3

y0

．线段AB的垂直平分线的方程是y-y0=-

y0

3

(x-2)，由此能求出直线AB的垂直平分线经过定点C（5，0）．
（2）直线AB的方程x=

y0

3

(y-y0)+2，代入y²=6x得y2-2y0y+2

y

2 0

-12=0，由此利用两点间距离公式和点到直线距离公式能求出△ABC面积的表达式．
（3）由（2）知S_△ABC=

1

3

1 2 (9+ y 2 0 )(24-2 y 2 0 )(9+ y 2 0 )

，由此利用均值定理能求出当且仅当9+

y

2 0

=24-2

y

2 0

时，△ABC面积的最大值为

14

3

7

．

解答： 解：（1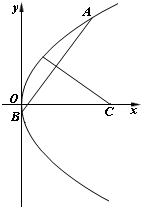）设线段AB的中点为M（x₀，y₀），
则 x0=

x1+x2

2

=2，y0=

y1+y2

2

，kAB=

y2-y1

x2-x1

=

y2-y1

y 2 2 6 - y 2 1 6

=

6

y2+y1

=

3

y0

．
线段AB的垂直平分线的方程是y-y0=-

y0

3

(x-2)，①
由题意知x=5，y=0是①的一个解，
所以线段AB的垂直平分线与x轴的交点C为定点，
且点C坐标为（5，0）．
所以直线AB的垂直平分线经过定点C（5，0）．…（4分）
（2）由①知直线AB的方程为y-y0=

3

y0

(x-2)，
即 x=

y0

3

(y-y0)+2，②
②代入y²=6x得y²=2y₀（y-y₀）+12，即y2-2y0y+2

y

2 0

-12=0，③
依题意，y₁，y₂是方程③的两个实根，且y₁≠y₂，
所以△=4

y

2 0

-4(2

y

2 0

-12)=-4

y

2 0

+48＞0，-2

3

＜y0＜2

3

．
|AB|=

(x1-x2)2+(y1-y2)2

=

(1+( y0 3 )2)(y1-y2)2

=

(1+ y 2 0 9 )[(y1+y2)2-4y1y2]

=

(1+ y 2 0 9 )(4 y 2 0 -4(2 y 2 0 -12))

=

2

3

(9+ y 2 0 )(12- y 2 0 )

．
定点C（5，0）到线段AB的距离h=|CM|=

(5-2)2+(0-y0)2

=

9+ y 2 0

．
∴S△ABC=

1

2

|AB|•h=

1

3

(9+ y 2 0 )(12- y 2 0 )

•

9+ y 2 0

…（8分）
（3）由（2）知S_△ABC=

1

3

1 2 (9+ y 2 0 )(24-2 y 2 0 )(9+ y 2 0 )

≤

1

3

1 2 ( 9+ y 2 0 +24-2 y 2 0 +9+ y 2 0 3 )3

=

14

3

7

，…（11分）
当且仅当9+

y

2 0

=24-2

y

2 0

，
即y0=±

5

，A(

6+ 35

3

，

5

+

7

)，B(

6- 35

3

，

5

-

7

)
或A(

6+ 35

3

，-(

5

+

7

))，B(

6- 35

3

，-

5

+

7

)时等号成立．
所以，△ABC面积的最大值为

14

3

7

．…（13分）

点评：本题考查直线的垂直平分线经过定点的证明，考查三角形面积的表达式的求法，考查三角形面积的最大值的求法，解题时要认真审题，注意均值定理的合理运用．