题目内容
7.若正数x,y满足$\frac{1}{y}+\frac{3}{x}=1$,则3x+4y的最小值是( )| A. | 24 | B. | 28 | C. | 25 | D. | 26 |
分析 利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵正数x,y满足$\frac{1}{y}+\frac{3}{x}=1$,
则3x+4y=(3x+4y)$(\frac{1}{y}+\frac{3}{x})$=13+$\frac{3x}{y}+\frac{12y}{x}$≥13+3×$2\sqrt{\frac{x}{y}×\frac{4y}{x}}$=25,当且仅当x=2y=5时取等号.
∴3x+4y的最小值是25.
故选:C.
点评 本题考查了“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
18.设全集U={x∈N|x<8},集合A={2,0,1,6},B={2,0,1,7},C={2,0,1,5},则∁U((A∩C)∪B)=( )
| A. | {2,0,1,7} | B. | {0,6,7,8} | C. | {2,3,4,5} | D. | {3,4,5,6} |
15.在△ABC中,M为边BC上的任意一点,点N在线段AM上,且满足$\overrightarrow{AN}=\frac{1}{3}\overrightarrow{NM}$,若$\overrightarrow{AN}=λ\overrightarrow{AB}+μ\overrightarrow{AC}({λ,μ∈R})$,则λ+μ的值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
19.已知定义在R上的函数f(x)的导函数为f′(x),对任意x∈R满足f(x)+f′(x)<0,则下列结论正确的是( )
| A. | 2f(ln2)>3f(ln3) | B. | 2f(ln2)<3f(ln3) | C. | 2f(ln2)≥3f(ln3) | D. | 2f(ln2)≤3f(ln3) |
16.若函数f(x)=(x-1)(x+2)(x2+ax+b)是偶函数,则f(x)的最小值为( )
| A. | -$\frac{25}{4}$ | B. | $\frac{7}{4}$ | C. | -$\frac{9}{4}$ | D. | $\frac{41}{4}$ |
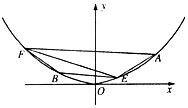 如图,已知线段AE,BF为抛物线C:x2=2py(p>0)的两条弦,点E、F不重合.函数y=ax(a>0且a≠1)的图象所恒过的定点为抛物线C的焦点.
如图,已知线段AE,BF为抛物线C:x2=2py(p>0)的两条弦,点E、F不重合.函数y=ax(a>0且a≠1)的图象所恒过的定点为抛物线C的焦点.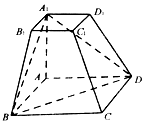 如图,在四棱台ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=2A1B1,AA1⊥平面ABCD.
如图,在四棱台ABCD-A1B1C1D1中,四边形ABCD是菱形,AB=2A1B1,AA1⊥平面ABCD.