题目内容
下列命题中真命题的是 ．
①?x∈（-∞，0），使得2x＜3x成立；
②命题“am2＜bm2，则a＜b”的逆命题是真命题；
③若￢P是q的必要条件，则P是￢q的充分条件；
④?x∈（0，π），则sinx＞cosx．
①?x∈（-∞，0），使得2x＜3x成立；
②命题“am2＜bm2，则a＜b”的逆命题是真命题；
③若￢P是q的必要条件，则P是￢q的充分条件；
④?x∈（0，π），则sinx＞cosx．
考点：命题的真假判断与应用
专题：简易逻辑
分析：①可以两边同除以2x，转化为(
)x，再结合x∈（-∞，0）判断与1的大小关系；
②关注m的符号进行判断；
③前后互为逆否命题，据此判断；
④举个反例如x=
代入，则sinx=cosx，所以④错．
| 3 |
| 2 |
②关注m的符号进行判断；
③前后互为逆否命题，据此判断；
④举个反例如x=
| π |
| 4 |
解答：
解：对于①，可以两边同除以2x，转化为(
)x，因为
＞1，所以当x∈（-∞，0）时，0＜(
)x＜1，因此2x＜3x，x∈（-∞，0）时恒成立，故①错；
对于②，逆命题是：若a＜b，则am2＜bm2，当m=0时，结论不成立，故②错；
对于③，因为￢P是q的必要条件，即q⇒￢p，其逆否命题是p⇒￢q成立，故p是￢q的充分条件，故③正确；
对于④，当x=
时，sinx=cosx，故④错误．
故答案为：③．
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
对于②，逆命题是：若a＜b，则am2＜bm2，当m=0时，结论不成立，故②错；
对于③，因为￢P是q的必要条件，即q⇒￢p，其逆否命题是p⇒￢q成立，故p是￢q的充分条件，故③正确；
对于④，当x=
| π |
| 4 |
故答案为：③．
点评：这道题考查了四种命题、全称命题及特称命题的真假判断及充分必要性的判断，要弄清条件和结论再解决问题．
练习册系列答案
阅读快车系列答案
相关题目
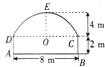如图所示的图形为一隧道的截面，其中ABCD是矩形，CED是抛物线的一段，在工程的设计中，要注意开凿隧道所需挖掘的土石方量，这就需要计算这个截面的面积，试根据图中所给出的数据计算这个截面的面积．
如图是一个边长为4的正方形及扇形（见阴影部分），若随机向正方形内丢一粒豆子，则豆子落入扇形的概率是（ ）A、
| ||
B、
| ||
C、
| ||
| D、π |