题目内容
向量
=（0，1，-1），
=（0，1，0），则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| A、0° | B、30° |
| C、45° | D、60° |
考点：空间向量的数量积运算
专题：空间向量及应用
分析：利用向量的夹角公式即可得出．
解答：
解：设
与
的夹角为θ．
•
=1，|
|=
，|
|=1．
∴cosθ=
=
=
，
∵θ∈[0，π]，∴θ=45°．
故选：C．
| a |
| b |
| a |
| b |
| a |
| 2 |
| b |
∴cosθ=
| ||||
|
|
| 1 | ||
|
| ||
| 2 |
∵θ∈[0，π]，∴θ=45°．
故选：C．
点评：本题考查了向量的夹角公式，属于基础题．
练习册系列答案
相关题目
设函数f（x）=log2x，则“a＞b”是“f（a）＞f（b）”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
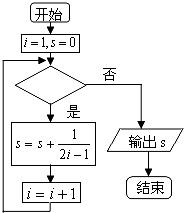如图给出的是计算1+| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2013 |
| A、i≤1006 |
| B、i＞1006 |
| C、i≤1007 |
| D、i＞1007 |
函数y=x2-x，（-1＜x＜4）值域是（ ）
A、[-
| ||
| B、（2，12） | ||
| C、（2，20） | ||
D、[-
|
若f（cosx）=
，x∈[0，π]，则f（-
）等于（ ）
| x |
| 2 |
| 1 |
| 2 |
A、cos
| ||
B、
| ||
C、
| ||
D、
|
若集合P∪{1，2，3}={1，2，3，4}，则满足条件的集合P的个数为（ ）
| A、6 | B、7 | C、8 | D、1 |
复数z满足
=1（i为虚数单位），则复数z为（ ）
| 1-zi |
| i |
| A、1+i | B、1-i |
| C、-1-i | D、-1+i |