题目内容
半径为5的球内包含有一个圆台,圆台的上、下两个底面都是球的截面圆,半径分别为3和4.则该圆台体积的最大值为 .
考点:旋转体(圆柱、圆锥、圆台)
专题:计算题,空间位置关系与距离
分析:由题意,圆台体积的最大时,圆台的上、下两个底面在球心的两侧,求出圆台的高,即可求出圆台体积的最大值
解答:
解:由题意,圆台体积的最大时,圆台的上、下两个底面在球心的两侧,
∵半径为5的球内包含有一个圆台,圆台的上、下两个底面都是球的截面圆,半径分别为3和4,
∴圆台的高为4+3=7,
∴圆台体积的最大值为
×7×(9π+12π+16π)=
π.
故答案为:
π.
∵半径为5的球内包含有一个圆台,圆台的上、下两个底面都是球的截面圆,半径分别为3和4,
∴圆台的高为4+3=7,
∴圆台体积的最大值为
| 1 |
| 3 |
| 259 |
| 3 |
故答案为:
| 259 |
| 3 |
点评:本题考查圆台体积的最大值,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)},(其中max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
| A、a2-2a-16 |
| B、a2+2a-16 |
| C、-16 |
| D、16 |
如图是某三棱锥的三视图,则这个三棱锥的体积是( )
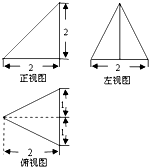

A、
| ||
B、
| ||
C、
| ||
D、
|