题目内容
2.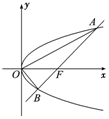 如图,过抛物线y2=2px(p>0)的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.
如图,过抛物线y2=2px(p>0)的焦点F作一条倾斜角为$\frac{π}{4}$的直线与抛物线相交于A,B两点.(1)用p表示|AB|;
(2)若$\overrightarrow{OA}$•$\overrightarrow{OB}$=-3,求这个抛物线的方程.
分析 (1)将直线方程与抛物线方程联立方程组,利用根与系数的关系和抛物线的定义得出|AB|;
(2)利用根与系数的关系用p表示出x1x2,y1y2,根据$\overrightarrow{OA}$•$\overrightarrow{OB}$=-3列方程解出p,从而得出抛物线方程.
解答 解:(1)抛物线的焦点为F($\frac{p}{2}$,0),过点F且倾斜角为$\frac{π}{4}$的直线方程为y=x-$\frac{p}{2}$.
联立方程组$\left\{\begin{array}{l}{{y}^{2}=2px}\\{y=x-\frac{p}{2}}\end{array}\right.$,得x2-3px+$\frac{{p}^{2}}{4}$=0,
设A(x1,y1),B(x2,y2),则x1+x2=3p,
∴|AB|=x1+x2+p=4p.
(2)由 (1)知x1+x2=3p,x1x2=$\frac{{p}^{2}}{4}$,
∴y1y2=(x1-$\frac{p}{2}$)(x2-$\frac{p}{2}$)=x1x2-$\frac{p}{2}$(x1+x2)+$\frac{{p}^{2}}{4}$=$\frac{{p}^{2}}{4}$-$\frac{3{p}^{2}}{2}$+$\frac{{p}^{2}}{4}$=-p2,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=$\frac{{p}^{2}}{4}$-p2=-$\frac{3{p}^{2}}{4}$=-3,解得p2=4,∴p=2.
∴抛物线的方程为y2=4x.
点评 本题考查了抛物线的定义与性质,直线与抛物线的位置关系,注意根与系数的关系运用,属于中档题.

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
| A. | (0,1) | B. | (-∞,1) | C. | (0,1] | D. | [0,1) |
| A. | $\frac{3}{2}$-$\frac{\sqrt{3}}{2}$i | B. | $\frac{3}{4}$-$\frac{\sqrt{3}}{4}$i | C. | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$i | D. | $\frac{3}{4}$+$\frac{\sqrt{3}}{4}$i |
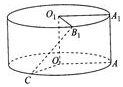 将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,∠AOC=120°,∠A1O1B1=60°,其中B1与C在平面AA1O1O的同侧,则异面直线B1C与AA1所成角的大小是45°.
将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,∠AOC=120°,∠A1O1B1=60°,其中B1与C在平面AA1O1O的同侧,则异面直线B1C与AA1所成角的大小是45°.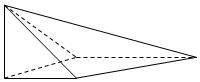 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=AD=1,BC=2.