题目内容
17.双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$两条渐近线l1、l2与抛物线y2=-4x的准线l围成区域Ω(包含边界),对于区域Ω内任一点(x,y),若$\frac{y+1}{x+3}$的最大值小于1,则双曲线C的离心率e的取值范围为(1,$\sqrt{10}$).分析 求得双曲线的渐近线方程和抛物线的准线方程,画出区域Ω,利用$\frac{y+1}{x+3}$的几何意义是点(x,y)与点P(-3,-1)的斜率,结合图象,连接PA,可得斜率最大,再由双曲线的a,b,c关系和离心率公式计算即可得到所求范围.
解答 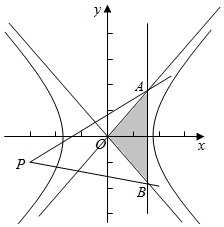 解:双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{b}{a}$x,
解:双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{b}{a}$x,
抛物线y2=-4x的准线1:x=1,
渐近线l1,l2与抛物线y2=-4x的准线1围成区域Ω,如图,
k=$\frac{y+1}{x+3}$的几何意义是点(x,y)与点P(-3,-1)的斜率,
求得A(1,$\frac{b}{a}$),B(1,-$\frac{b}{a}$),
连接PA,可得斜率最大为k=$\frac{\frac{b}{a}+1}{4}$,
由题意可得$\frac{\frac{b}{a}+1}{4}$<1,
可得$\frac{b}{a}$<3,即3a>b,9a2>b2=c2-a2,
即c2<10a2,即有c<$\sqrt{10}$a.
可得1<e<$\sqrt{10}$.
故答案为:(1,$\sqrt{10}$).
点评 本题考查双曲线和抛物线的性质,考查双曲线的离心率的范围,注意运用数形结合的思想方法,考查直线的斜率的范围,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
7.“x≠y”是“|x|≠|y|”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.已知函数f(x)=sin(2x+$\frac{π}{4}$),则下列结论中正确的是( )
| A. | 函数f(x)的最小正周期为2π | |
| B. | 函数f(x)的图象关于点($\frac{π}{4}$,0)对称 | |
| C. | 由函数f(x)的图象向右平移$\frac{π}{8}$个单位长度可以得到函数y=sin2x的图象 | |
| D. | 函数f(x)在区间($\frac{π}{8}$,$\frac{5π}{8}$)上单调递增 |
5.在(1+$\frac{x}{2}$)(1+$\frac{x}{{2}^{2}}$)…(1+$\frac{x}{{2}^{n}}$)(n∈N+,n≥2)的展开式中,x的系数为$\frac{15}{16}$,则x2的系数为( )
| A. | $\frac{15}{16}$ | B. | $\frac{31}{128}$ | C. | $\frac{35}{128}$ | D. | $\frac{31}{64}$ |
9.设全集U={x∈N*|x≤5},A={1,4},B={4,5},则∁U(A∩B)=( )
| A. | {1,2,3,5} | B. | {1,2,4,5} | C. | {1,3,4,5} | D. | {2,3,4,5} |