题目内容
18.已知双曲线C与双曲线$\frac{{y}^{2}}{2}$-x2=1有相同的渐近线,且C的一个顶点为(1,0),C的焦点为F1,F2,在曲线C上有一点M满足$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0,求点M到x轴的距离.分析 求出双曲线的方程,由$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0得MF1⊥MF2,可知点M在以F1F2为直径的圆x2+y2=3上,由此可以推导出点M到x轴的距离.
解答 解:∵双曲线C与双曲线$\frac{{y}^{2}}{2}$-x2=1有相同的渐近线,
∴设双曲线C:$\frac{{y}^{2}}{2}$-x2=λ,
∵C的一个顶点为(1,0),
∴λ=-1,
∴双曲线C:x2-$\frac{{y}^{2}}{2}$=1的焦点为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0).
又∵$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0,
∴MF1⊥MF2,∴点M在以F1F2为直径的圆x2+y2=3上
故与x2-$\frac{{y}^{2}}{2}$=1联立得|y|=$\frac{2\sqrt{3}}{3}$,
∴点M到x轴的距离为$\frac{2\sqrt{3}}{3}$.
点评 本题考查双曲线的性质及其应用,解题时要注意挖掘隐含条件.

练习册系列答案
相关题目
9.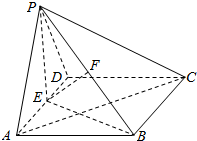 如图,已知平面PAD⊥平面ABCD,ABCD为矩形,PA=PD,AD=$\sqrt{2}$AB,E是线段AD的中点,F是线段PB的中点.
如图,已知平面PAD⊥平面ABCD,ABCD为矩形,PA=PD,AD=$\sqrt{2}$AB,E是线段AD的中点,F是线段PB的中点.
(1)求证:EF∥平面PCD;
(2)求证:AC⊥平面PBE.
 如图,已知平面PAD⊥平面ABCD,ABCD为矩形,PA=PD,AD=$\sqrt{2}$AB,E是线段AD的中点,F是线段PB的中点.
如图,已知平面PAD⊥平面ABCD,ABCD为矩形,PA=PD,AD=$\sqrt{2}$AB,E是线段AD的中点,F是线段PB的中点.(1)求证:EF∥平面PCD;
(2)求证:AC⊥平面PBE.
6.在平面四边形ABCD中,∠A=∠B=60°,∠C=75°,BC=2,则AB的取值范围是( )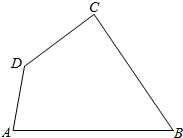

| A. | ($\sqrt{3}$-1,2) | B. | (2,$\sqrt{3}$+1) | C. | ($\sqrt{3}$-1,$\sqrt{3}$+1) | D. | (2,4) |
7.若a,b∈(0,1),则函数f(x)=x2-2ax+b在R上没零点的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |