题目内容
在棱长为2的正方体中,点E,F分别是棱AB,BC的中点,则点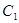 到平面
到平面 的距离等于( )
的距离等于( )
A.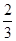 | B.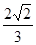 | C.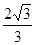 | D. |
D
解析试题分析:利用勾股定理、三棱锥的体积、等积变形即可得出.解:如图所示:
由BE⊥BF,BE=BF=1,∴EF= .同理,B1E=B1F=
.同理,B1E=B1F= ,∴S△B1EF=
,∴S△B1EF=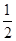 ×
× ×
× =
= 又知道S△B1C1F=
又知道S△B1C1F=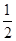 ×22=2,EB⊥平面BCC1B1.∴VC1-B1EF=VE-B1C1F,∴
×22=2,EB⊥平面BCC1B1.∴VC1-B1EF=VE-B1C1F,∴ ×S△B1EF×hC1=
×S△B1EF×hC1= ×S△B1C1F×EB,∴
×S△B1C1F×EB,∴ ×
× ×hC1=
×hC1= ×2×1,解得hC1=
×2×1,解得hC1= 故选D.
故选D.
考点:三棱锥的体积
点评:熟练掌握三棱锥的体积计算公式及等积变形是解题的关键.

练习册系列答案
相关题目
设x、y、z是空间中不同的直线或平面,对下列四种情形:
①x、y、z均为直线;②x、y是直线,z是平面;③z是直线,x、y是平面;④x、y、z均为平面,其中使“x⊥z且y⊥z⇒x∥y”为真命题的是 ( )
| A.③④ | B.①③ |
| C.②③ | D.①② |
关于两条不同的直线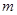 ,
, 与两个不同的平面
与两个不同的平面 ,
, ,下列正确的是( )
,下列正确的是( )
A. 且 且 ,则 ,则 |
B. 且 且 ,则 ,则 |
C. 且 且 ,则 ,则 |
D. 且 且 ,则 ,则 |
在三棱柱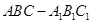 中,各侧面均为正方形,侧面
中,各侧面均为正方形,侧面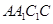 的对角线相交于点
的对角线相交于点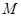 ,则
,则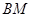 与平面
与平面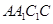 所成角的大小是( )
所成角的大小是( )
| A.30° | B.45° | C.60° | D.90 |
如图,在正方体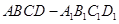 中,
中,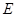 、
、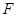 分别为棱
分别为棱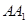 、
、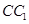 的中点,则在空间中与直线
的中点,则在空间中与直线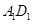 、
、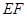 、CD都相交的直线有
、CD都相交的直线有
| A.1条 | B.2条 | C.3条 | D.无数条 |
如图,在长方体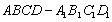 中,
中, ,
, ,则异面直线
,则异面直线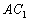 与
与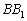 所成的角为 ( )
所成的角为 ( )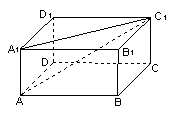
A.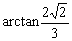 | B. | C.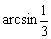 | D.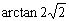 |




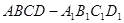 的面对角线
的面对角线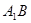 上存在一点
上存在一点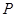 使得
使得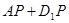 最短,则
最短,则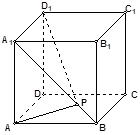
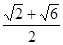
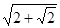
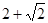
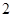
 ABC的边AB,BC,CA的中点,O是△ABC的重心,则
ABC的边AB,BC,CA的中点,O是△ABC的重心,则 ( )
( )



