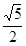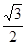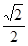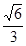题目内容
设x、y、z是空间中不同的直线或平面,对下列四种情形:
①x、y、z均为直线;②x、y是直线,z是平面;③z是直线,x、y是平面;④x、y、z均为平面,其中使“x⊥z且y⊥z⇒x∥y”为真命题的是 ( )
| A.③④ | B.①③ |
| C.②③ | D.①② |
C
解析试题分析:因为,x、y、z均为直线,x,y,z不一定在同一平面内,所以,x⊥z且y⊥z⇒x∥y是假命题,即①不合题意;
因为,x、y是直线,z是平面,所以,x⊥z且y⊥z时,x//y,即②符合题意;
因为,z是直线,x、y是平面,所以,x⊥z且y⊥z时,垂直于同一直线的两平面平行,
x∥y,即③符合题意,故选C。
考点:命题,立体几何平行关系、垂直关系。
点评:简单题,涉及命题真假判断问题,往往综合性较强,须灵活应用所学知识解题。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
在四边形 中,
中, ∥
∥ ,
, ,将
,将 沿
沿 折起,使平面
折起,使平面 平面
平面 ,构成三棱锥
,构成三棱锥 ,则在三棱锥
,则在三棱锥 中,下列命题正确的是( )
中,下列命题正确的是( )
A.平面 平面 平面 | B.平面 平面 平面 |
C.平面 平面 平面 | D.平面 平面 平面 |
对于不重合的直线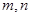 和不重合的平面
和不重合的平面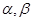 ,下列命题错误的是( )
,下列命题错误的是( )
A.若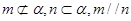 ,则 ,则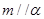 | B.若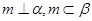 ,则 ,则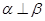 |
C.若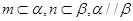 ,则 ,则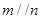 | D.若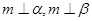 ,则 ,则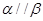 |
设 、
、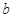 是两条不同的直线,
是两条不同的直线,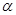 、
、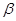 是两个不同的平面,给出下列结论:
是两个不同的平面,给出下列结论:
① ∥
∥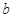 ,
,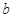
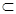
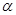 ⇒
⇒ ∥
∥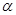 ;
;
②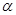 ∥
∥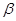 ,
, ∥
∥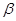 ,
,

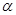 ⇒
⇒ ∥
∥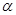 ;
;
③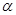

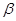 =
= ,
,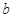 ∥
∥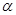 ,
,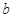 ∥
∥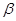 ⇒
⇒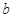 ∥
∥ ;
;
④ ∥
∥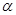 ,
,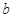
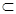
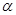 ⇒
⇒ ∥
∥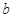 .
.
其中正确的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
对于直线 ,
, 和平面
和平面 ,
, ,使
,使 成立的一个充分条件是
成立的一个充分条件是
A. , , ∥ ∥ | B. ∥ ∥ , , |
C. , , , , | D. , , , , |
用 、
、 、
、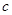 表示三条不同的直线,
表示三条不同的直线,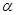 表示平面,给出下列命题:
表示平面,给出下列命题:
①若 ∥
∥ ,
, ∥
∥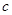 ,则
,则 ∥
∥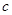 ; ②若
; ②若 ⊥
⊥ ,
, ⊥
⊥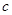 ,则
,则 ⊥
⊥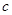 ;
;
③若 ∥
∥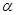 ,
, ∥
∥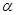 ,则
,则 ∥
∥ ; ④若
; ④若 ⊥
⊥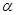 ,
, ⊥
⊥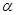 ,则
,则 ∥
∥ .
.
| A.①② | B.②③ | C.①④ | D.③④ |
在棱长为2的正方体中,点E,F分别是棱AB,BC的中点,则点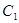 到平面
到平面 的距离等于( )
的距离等于( )
A.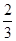 | B.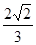 | C.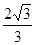 | D. |
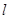 与平面
与平面 有公共点”是真命题,那么下列命题:
有公共点”是真命题,那么下列命题: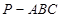 中,
中,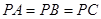 ,底面
,底面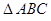 是正三角形,
是正三角形,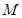 、
、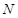 分别是侧棱
分别是侧棱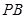 、
、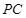 的中点. 若平面
的中点. 若平面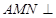 平面
平面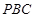 ,则侧棱
,则侧棱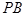 与平面
与平面 所成角的正切值是( )
所成角的正切值是( )