题目内容
函数f(x)=cos3x+sin2x-cosx上最大值等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:利用换元法将函数进行换元,求函数的导数,利用导数和函数最值之间的关系即可得到结论.
解答:
解:f(x)=cos3x+sin2x-cosx=cos3x+1-cos2x-cosx,
令t=cosx,则-1≤t≤1,
则函数f(x)等价为g(t)=t3+1-t2-t,-1≤t≤1
函数的导数g′(t)=3t2-2t-1=(t-1)(3t+1),-1≤t≤1,
当-
≤t≤1时,g′(t)≤0,函数单调递减,
当-1≤t≤-
时,g′(t)≥0,函数单调递增,
则t=-
,函数g(t)取得极大值,同时也是最大值g(-
)=
,
故选:D.
令t=cosx,则-1≤t≤1,
则函数f(x)等价为g(t)=t3+1-t2-t,-1≤t≤1
函数的导数g′(t)=3t2-2t-1=(t-1)(3t+1),-1≤t≤1,
当-
| 1 |
| 3 |
当-1≤t≤-
| 1 |
| 3 |
则t=-
| 1 |
| 3 |
| 1 |
| 3 |
| 32 |
| 27 |
故选:D.
点评:本题主要考查函数的最值,利用换元法,结合函数最值和函数导数之间的关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a,b是不同的直线,α,β是不同的平面,则下列结论错误的是( )
| A、若a⊥α,b∥α,则a⊥b |
| B、若a⊥α,b⊥β,α∥β,则a∥b |
| C、若a⊥α,b∥α,b?β,则a⊥β |
| D、若a⊥α,a⊥β,则α∥β |
若z1=(m2+m+1)+(m2+m-4)i,m∈R,z2=3-2i,则m=1是z1=z2的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
| ∫ | 1 -1 |
| A、0 | ||
| B、1 | ||
| C、2cos1 | ||
D、
|
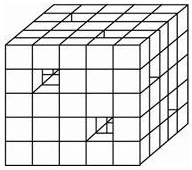 如图所示,棱长为6的正方体无论从哪一个面看,都有两个直通的边长为l的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )
如图所示,棱长为6的正方体无论从哪一个面看,都有两个直通的边长为l的正方形孔,则这个有孔正方体的表面积(含孔内各面)是( )| A、222 | B、258 |
| C、312 | D、324 |
若
=(1,2),
=(-1,1),
=(2,1),k
+
与
共线,则k的值为( )
| a |
| b |
| c |
| a |
| b |
| c |
| A、2 | B、1 | C、0 | D、-1 |