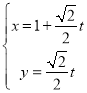题目内容
【题目】若直线l的极坐标方程为![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() (
(![]() 为参数).
为参数).
![]() 若曲线上存在M,N两点关于直线l对称,求实数m的值;
若曲线上存在M,N两点关于直线l对称,求实数m的值;
![]() 若直线与曲线相交于P,Q两点,且
若直线与曲线相交于P,Q两点,且![]() ,求实数m的取值范围.
,求实数m的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
![]() 直接利用参数方程直角坐标方程和极坐标方程之间的转换进一步利用对称关系的应用求出结果.
直接利用参数方程直角坐标方程和极坐标方程之间的转换进一步利用对称关系的应用求出结果.
![]() 利用直线和圆的位置关系的应用建立不等量关系求出参数m的取值范围.
利用直线和圆的位置关系的应用建立不等量关系求出参数m的取值范围.
解:![]() 直线l的极坐标方程为
直线l的极坐标方程为![]() ,
,
化为直角坐标方程得![]() .
.
曲线C的参数方程为![]() 为参数
为参数![]() .
.
化为普通方程得![]() .
.
从而得到圆心为![]() ,半径为3.
,半径为3.
根据题意知圆心![]() 在直线l上
在直线l上
则![]() ,
,
即![]() .
.
![]() 设圆心到直线l的距离为d,
设圆心到直线l的距离为d,
则![]() .
.
所以解得![]() 由点到直线距离公式得:
由点到直线距离公式得:
![]()
解得![]() 或
或![]() ,
,
又直线与圆必须相交,则![]() 即
即![]()
解得![]() .
.
综上,满足条件的实数m的取值范围是![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目