题目内容
【题目】在平面坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线
轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)把曲线![]() 的方程化为普通方程,
的方程化为普通方程,![]() 的方程化为直角坐标方程
的方程化为直角坐标方程
(2)若曲线![]() ,
,![]() 相交于
相交于![]() 两点,
两点,![]() 的中点为
的中点为![]() ,过
,过![]() 点作曲线
点作曲线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
![]() 利用代入法消去参数可得到曲线
利用代入法消去参数可得到曲线![]() 的普通方程,利用
的普通方程,利用![]() 可得
可得![]() 的直角坐标方程;
的直角坐标方程;![]() 利用
利用![]() 的结论,利用一元二次方程根和系数关系求得线段AB的中垂线参数方程为
的结论,利用一元二次方程根和系数关系求得线段AB的中垂线参数方程为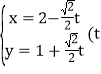 为参数
为参数![]() ,代入
,代入![]() ,利用直线参数方程的几何意义可得结果.
,利用直线参数方程的几何意义可得结果.
![]() 曲线
曲线![]() 的参数方程为
的参数方程为![]() 其中t为参数
其中t为参数![]() ,转换为直角坐标方程为:
,转换为直角坐标方程为:![]() .
.
曲线![]() 的极坐标方程为
的极坐标方程为![]() .转换为直角坐标方程为:
.转换为直角坐标方程为:![]() .
.
![]() 设
设![]() ,
,![]() ,且中点
,且中点![]() ,联立方程为:
,联立方程为:![]() ,
,
整理得:![]() 所以:
所以:![]() ,
,![]() ,由于:
,由于:![]() ,
,![]() .
.
所以线段AB的中垂线参数方程为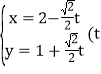 为参数
为参数![]() ,代入
,代入![]() ,
,
得到:![]() ,故:
,故:![]() ,
,![]() ,
,
所以:![]() ,
,![]()
故:![]() .
.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|