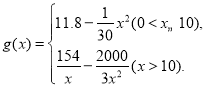Question

【题目】函数（a为常数，且）在处取得极值．

（1）求实数a的值，并求的单调区间；

（2）关于x的方程在上恰有1个实数根，求实数b的取值范围；

（3）求证：当时，．

Answer 1

【答案】（1），的单调递增区间是，函数的单调递减区间是．（2）．（3）见解析

【解析】

（1）首先写出函数的定义域，之后求函数的导函数，利用条件，得到等式，解出，代入导函数解析式，令，，求得函数的单调增、减区间；

（2）将的解析式代入方程，化简得，令，利用导数研究其单调性，结合题意，得到不等式组，求得结果；

（3）结合（1），得到，进一步得到成立，对依次取值，累加得到结果.

（1），，由题意得，，

得，

当时，，

令，得，

令，得，

∴函数的单调递增区间是，

函数的单调递减区间是．

（2）关于x的方程，

化简为，

令，

，

令，解得或1，

令，得，

函数在上单调递增，

关于x的方程在上恰有1个实数根，

则只需

得．

（3）由（1）知，当时，，即，

当时，令，则成立，

即成立

将n依次取1，2，3，4，5，…………，

可得，

，

……

，

，

累加求和得：，

即当时，成立．