题目内容
已知△ABC三个内角A,B,C成等差数列,且AB=1,BC=4,则边AC上的高h=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:等差数列的性质
专题:综合题,等差数列与等比数列,解三角形
分析:先根据三个内角A、B、C成等差数列和三角形内角和为π可求得B的值,进而利用余弦定理求出AC,利用三角形的面积公式,即可得出结论.
解答:
解:∵△ABC的三个内角A、B、C成等差数列,
∴2B=A+C,又A+B+C=180°,
∴∠ABC=60°,AB=1,BC=4,
根据余弦定理得:AC=
,
∴
×1×4×
=
×
h
∴h=
.
故选:A.
∴2B=A+C,又A+B+C=180°,
∴∠ABC=60°,AB=1,BC=4,
根据余弦定理得:AC=
| 13 |
∴
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 13 |
∴h=
| 2 |
| 13 |
| 39 |
故选:A.
点评:本题主要考查等差中项和余弦定理,涉及三角形的内角和定理,难度一般.

练习册系列答案
相关题目
(-i)2是( )
| A、虚数 | B、纯虚数 | C、1 | D、-1 |
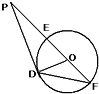 如图,已知P是⊙O外一点,PD为⊙O的切线,D为切点,割线PEF经过圆心O.若PF=16,PD=4
如图,已知P是⊙O外一点,PD为⊙O的切线,D为切点,割线PEF经过圆心O.若PF=16,PD=4| 3 |
| A、13 | B、6.5 | C、7 | D、8 |
求值:cos2
-sin2
=( )
| π |
| 12 |
| π |
| 12 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、-
|
将函数y=2sin2(x-
)图象所有点横坐标缩短为原来一半,再向右平移
,得到函数f(x)的图象,那么关于f(x)的论断正确的是( )
| π |
| 3 |
| π |
| 3 |
A、周期为
| ||||
B、周期为
| ||||
C、最大值为2,一个对称轴为x=
| ||||
D、最大值为1,一个对称轴为x=
|
已知点(-1,2)和(3,-3)在直线3x+y-a=0的同侧,则a取值范围( )
| A、(-1,6) |
| B、(-6,1) |
| C、(-∞,-1)∪(6,+∞) |
| D、(-∞,-6)∪(1,+∞) |
若a>b,则下列不等式一定成立的是( )
| A、2a>2b | ||||
| B、a2>b2 | ||||
| C、ac>bc | ||||
D、
|
直线l1:(2-a)x+ay+3=0和直线l2:x-ay-3=0,若直线l1的法向量恰好是直线l2的方向向量,则实数a的值为( )
| A、-2 | B、1 | C、-2或1 | D、0 |